Lexikon der Mathematik: Integralexponentialfunktion
die für x ∈ ℝ\{0} durch
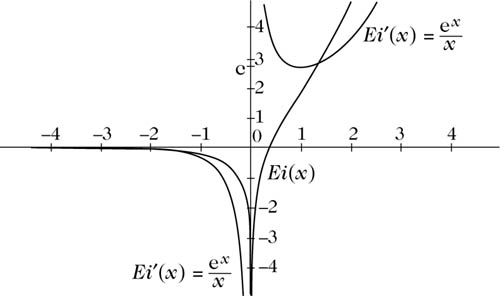
Integralexponentialfunktion
Für x ∈ ℝ\{0} gilt
Die Funktion Ei ist zu einer in der geschlitzten Ebene \({{\mathbb{C}}}^{-}={\mathbb{C}}\backslash (-\infty, 0]\) holomorphen Funktion fortsetzbar. Bezeichnet Log den Hauptzweigdes Logarithmus, so ist Eiz − Log z zu einer ganz transzendenten Funktion fortsetzbar. Für z ∈ ℂ− gilt die Reihenentwicklung
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.