Körper, der entsteht, wenn ein Kreiskegel mit zwei zur Achse des Kegels senkrechten Ebenen ε₁ und ε₂ geschnitten wird (wobei ε₁ und ε₂ die Kegelachse auf derselben Seite bezüglich der Spitze des Kreiskegels schneiden).

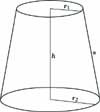
Der Abstand der Ebenen ε₁ und ε₂ heißt Höhe h, und die Radien r₁, r₂ der beiden entstehen Schnittkreise des Kegels mit den beiden Ebenen heißen Radien des Kegelstumpfes.

Die Länge der Mantellinien eines Kegelstumpfes mit der Höhe h und den Radien r₁, r₂ ist \begin{eqnarray}s=\sqrt{{({r}_{2}-{r}_{1})}^{2}+{h}^{2}},\end{eqnarray} für seine Mantelfläche gilt \begin{eqnarray}{A}_{M}=\pi \cdot s\cdot ({r}_{1}+{r}_{2}).\end{eqnarray}--> Der gesamte Oberflächeninhalt eines Kegelstumpfes beträgt \begin{eqnarray}{A}_{O}=\pi \cdot ({r}_{1}^{2}+{r}_{2}^{2}+s.({r}_{1}+{r}_{2})),\end{eqnarray} und für sein Volumen gilt \begin{eqnarray}V=\frac{\pi }{3}\cdot h\cdot ({r}_{1}^{2}+{r}_{2}^{2}+{r}_{1}{r}_{2}).\end{eqnarray}