die Einteilung kompakter komplexer Flächen (2-dimensionaler komplexer Mannigfaltigkeiten).

Wenn κ(X) die Kodaira-Dimension bezeichnet, so gibt es in jeder Klasse von birational äquivalenten (oder bimeromorph äquivalenten) Flächen ausgezeichnete glatte Modelle, die im Falle κ(X) ≥ 0 bis auf Isomorphie eindeutig bestimmt sind. Eine Grobstruktur dieser Modelle wird durch die Klassifikation beschrieben, gewöhnlich als Enriques-Klassifikation oder Enriques-Kodaira-Klassifikation bezeichnet. Zur Klassifikation werden neben der Kodaira-Dimension noch die Plurigeschlechter (Kodaira-Dimension) P_m(X), (wobei es ausreicht, P₁(X) = p_g(X), geometrisches Geschlecht genannt, und P₁₂(X) zu betrachten), die Irregularität q(X) = dim H¹(X, 𝒪_X) sowie die erste Betti-Zahl b₁(X) herangezogen.

Die Klassifikation sagt aus, welche Kombinationen dieser Invarianten vorkommen, und erlaubt in den meisten Fällen auch eine genauere Beschreibung der Struktur dieser Flächen. Die Invarianten sind (für Flächen) alle invariant unter Deformationen.

Wichtige topologische Invarianten sind die Chern-Zahlen (Chern-Klassen) \(({c}_{1}^{2})\,\,=\,\,({K}_{X}^{2})\), (Selbstschnittzahl der kanonischen Klasse) und c₂ = e (topologische Euler-Charakteristik).

Folgende Relationen bestehen zwischen diesen Invarianten: \begin{eqnarray}\begin{array}{l}12(1\,-\,q\,+\,{p}_{g})\,=\,({K}^{2})\,+\,e\,\,\,(\text{Max}\,\text{Noether}),\\ \frac{({K}^{2})\,-\,2e}{3}\,=\,\sigma \,\,\,(\text{F}.\,\text{Hirzebruch}),\,.\\ ({K}^{2})\,\le \,3e\,\,\,(\text{Miyaoka-Yau}),\\ ({K}^{2})\,\ge \,2p_g\,-\,4\,\,\,(\text{Max}\,\text{Noether});\end{array}\end{eqnarray}

Hierbei ist σ die Signatur des Schnittproduktes auf H²(X, ℝ) (oder H₂(X, ℝ)). Die letzten beiden Ungleichungen beziehen sich auf minimale Modelle.

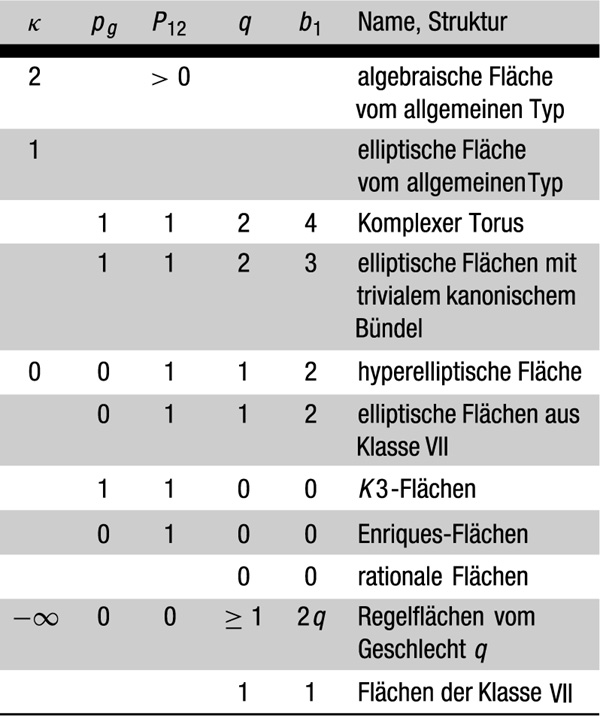
Es ergibt sich folgende Tabelle:

Dabei ist (K²) > 0 für Flächen vom allgemeinen Typ, (K²) = 0 für Flächen mit κ(X) = 0 oder 1, (K²) = 8(1 − q) für Regelflächen, (K²) = 9 für ℙ² und (K²) ≤ 0 für Flächen der Klasse VII. e ergibt sich dann aus Noethers Formel.

Hierbei versteht man unter einer Regelfläche vom Geschlecht q eine Faserung X → B über einer glatten Kurve B vom Geschlecht q mit der allgemeinen Faser ℙ¹. Eine elliptische Fläche ist eine Fläche mit einer Faserung \(X\,\mathop{\to }\limits^{p}\,B\), deren allgemeine Fasern elliptische Kurven sind. Wenn κ(X) = 1 ist und R_•(X) den kanonischen Ring bezeichnet, erhält man eine ausgezeichnete derartige Faserung durch die Kodaira-Faserung X → B = Proj (R_•(X)). Solche elliptischen Faserungen heißen „elliptisch vom allgemeinen Typ“. Hyperelliptische Flächen sind Flächen mit einer elliptischen Faserung X → B über einer elliptischen Kurve so, daß alle Fasern isomorph zu einer elliptischen Kurve F sind und b₁(X) = 2 ist. Diese Flächen sind algebraisch und besitzen eine abelsche Fläche als unverzweigte Überlagerung.

K3-Flächen sind einfach zusammenhängende Flächen, auf denen eine nirgends verschwindende holomorphe 2-Form existiert. Beispiele sind glatte Flächen vom Grad 4 im ℙ³ und Doppelüberlagerungen der projektiven Ebene mit einer Verzweigungskurve vom Grad 6. Alle K3-Flächen sind diffeomorph zueinander und besitzen eine Kähler-Metrik.

Enriques-Flächen sind solche, die man als Quotienten von K3-Flächen nach einer fixpunktfreien holomorphen Involution erhält. Sie sind alle algebraisch, und die Isomorphieklassen „bilden“ eine 10-dimensionale komplex-analytische Familie. Bemerkenswert ist, daß die Existenz von Enriques-Flächen zeigt, daß die Bedingung p_g(= P₁) = 0 und q = 0 nicht ausreicht, um Rationalität zu charakterisieren.

Am wenigsten bekannt sind Flächen der Klasse VII, Beispiele dafür sind Hopf-Flächen (Flächen mit der universellen Überlagerung ℂ² \ {0}, z. B. Quotienten nach der von einem Automorphismus (z₁, z₂) ↦ (α₁z₁, α₂z₂) mit 0 < |α₁| ≤ |α₂| < 1 erzeugten zyklischen Gruppe; solche Quotienten sind diffeomorph zu S¹ × S³).

Die Klasse der Flächen vom allgemeinen Typ ist die größte Klasse. Ihre Klassifizierung würde auf die Klassifizierung der entsprechenden kanonischen Ringe (Kodaira-Dimension) hinauslaufen, da sie vollständig durch diese bestimmt sind.