geschlossene nichtorientierbare Fläche mit dem Geschlecht (Genus) g = 1.

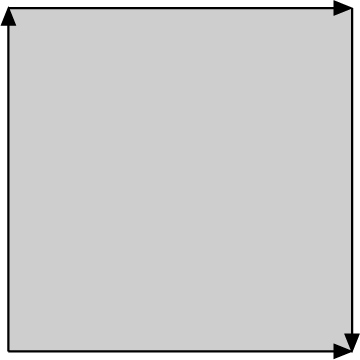
Diese Fläche besitzt kein Inneres und kein Äußeres. Sie kann konstruiert werden, indem beide Paare gegenüberliegender Ecken eines Rechtecks zusammengeklebt werden, wobei ein Paar eine halbe Drehung erhält (siehe Abb. 1). Eine wirkliche Realisierung dieser Konstruktion ist jedoch nur im 4-dimensionalen Raum möglich, da sich die Fläche selbst durchdringen muß, ohne ein Loch zu besitzen.

Eine mögliche Abbildung einer Kleinschen Flasche in den dreidimensionalen Raum ist durch die Parameterdarstellung \begin{array}{l}x(u,v)=\left[a+\cos \frac{u}{2}\,\,\sin v-\sin \frac{u}{2}\,\,\sin (2v)\right]\,\cos\,u\\ y(u,v)=\left[a+\cos \frac{u}{2}\,\,\sin v-\sin \frac{u}{2}\,\,\sin (2v)\right]\,\sin\,u\\ z(u,v)=\,\,\sin \frac{u}{2}\,\,\sin v+\cos \frac{u}{2}\,\,\sin (2v)\end{array}

(mit u ∈ [0, 2π), v ∈ [0, 2π) und a ≥ 2) gegeben. Die dadurch realisierte Abbildung der Kleinschen Flasche in den ℝ³ zeigt Abb. 2 (wobei die Fläche mit der o.a. Parameterdarstellung normalerweise geschlossen ist, zur besseren Veranschaulichung wurde für die Abbildung v ∈ [−0, 25π, 1, 6π] gewählt). Eine derartige Kleinsche Flasche läßt sich durch die Drehung einer Acht-Kurve um eine Achse bei gleichzeitiger Drehung um ihren Mittelpunkt konstruieren.

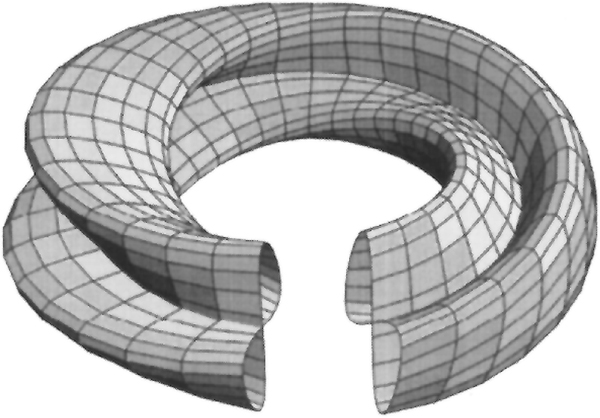
Eine weitere mögliche Darstellung der Kleinschen Flasche im ℝ³ ist durch die Parametergleichung \begin{array}{l}x(u,v)=\,\,\cos u\left[(\sqrt{2}+\cos v)\cos \frac{u}{2}+\sin v\cos v\,\sin \frac{u}{2}\right]\\ y(u,v)=\sin u\left[(\sqrt{2}+\cos v)\cos \frac{u}{2}+\sin v\cos v\,\sin \frac{u}{2}\right]\\ z(u,v)=\,-\left(\sqrt{2}+\cos v\right)\sin \frac{u}{2}+\cos \frac{u}{2}\,\sin v\,\cos v\end{array}

oder durch die implizite Gleichung \begin{eqnarray}\left({x}^{2}+{y}^{2}+{z}^{2}+2y-1\right)\left[{\left({x}^{2}+{y}^{2}+{z}^{2}-2y-1\right)}^{2}-8{z}^{2}\right]+16xz\,\left({x}^{2}+{y}^{2}+{z}^{2}-2y-1\right)=0\end{eqnarray}

gegeben (siehe Abb. 3).