Lexikon der Mathematik: Klothoide
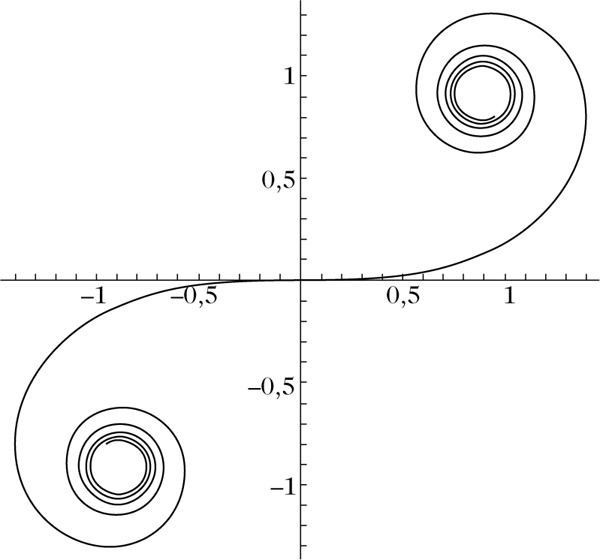
Spinnkurve, Cornusche Spirale, ebene Kurve, deren Krümmung eine lineare Funktion der Bogenlänge ist.
Ist α(s) = (x(s), y(s)) eine Parametergleichung einer Klothoide, wobei der Parameter s gleichzeitig die Bogenlänge, gemessen von einem festen Kurvenpunkt α(s0) an ist, so hat die Krümmungsfunktion der Kurve die Gestalt
Die Klothoide wickelt sich in beiden Richtungen spiralartig um einen festen Punkt. Durch Lösen der natürlichen Gleichungen ergibt sich folgende analytische Darstellung durch Fresnel-Integrale:
Wenn die Winkelstellung der gelenkten Räder eines Fahrzeugs zur Fahrzeugachse bei konstanter Fahrgeschwindigkeit gleichmäßig (linear) wächst, man denke z. B. an die Drehungen des Lenkrades beim Autofahren, so ist die durchfahrene Kurve ein klothoidisches Kurvenstück, da dieser Winkel ein Maß für die Krümmung der Kurve darstellt.
Klothoide
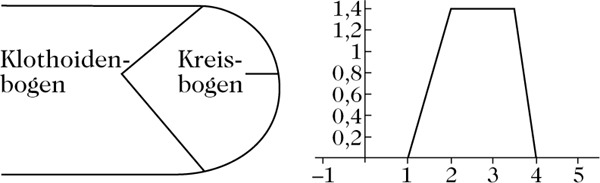
Wende um 180○ mit zwei klothoiden Anrampungen und die zugehörige Krümmungsfunktion.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.