Knoten sind Bestandteil der menschlichen Kultur. Im täglichen Leben benutzt man sie seit Jahrtausenden zum Binden von Schnüren und dergleichen, heute z. B. bei Schiffstauen, Schuhriemen und Gürteln. Auch in der Kunst findet man Knoten. In Gestalt der Quipus dienten sie bei den Inkas sogar als Symbole für Zahlen.

Die Knotentheorie als mathematische Disziplin ist Teil der drei-dimensionalen Topologie. Ihre Ausstrahlungen in die übrige Topologie, in andere Felder der Mathematik und in die Naturwissenschaften einerseits, die von diesen ausgehenden Anregungen, ja Herausforderungen andererseits stehen beispielhaft für die gegenseitige Verflechtung, die die Entwicklung der Wissenschaften in fruchtbarer Weise begleitet.

In der mathematischen Knotentheorie versteht man unter einem Knoten im einfachsten Fall eine geschlossene Kurve im drei-dimensionalen Raum, d. h. eine zur Kreislinie homöomorphe Teilmenge des ℝ³ [3]. Zwei solche Knoten heißen äquivalent, wenn ein orientierungserhaltender Homöomorphismus des drei-dimensionalen Raumes auf sich selbst existiert, der den einen Knoten in den anderen überführt. Als Beispiel stelle man sich die Verformung (Isotopie) eines Knotens in einen anderen vor, wobei während der Verformung immer ein Knoten vorliegen soll, also etwa zwischenzeitliches Durchtrennen des Knotens nicht erlaubt ist. Äquivalente Knoten bilden eine Äquivalenzklasse und werden als nicht wesentlich verschieden betrachtet. Aus dem Wunsch nach einer Systematik aller Knoten heraus stellt sich die Aufgabe der Klassifikation der Knoten; das ist im Idealfall die Angabe genau eines Repräsentanten (d. h. eines Beispiels) in jeder Äquivalenzklasse, sowie eine Methode, um für zwei beliebige Knoten zu entscheiden, ob sie äquivalent sind. Die zuletzt genannte Unterscheidung zweier Knoten kann z. B. durch eine Knoteninvariante geleistet werden. Sie ordnet gewissen Knoten Werte zu (Zahlen, Farben oder andere Objekte), und zwar in der Weise, daß äquivalenten Knoten der gleiche Wert zukommt. Sind für zwei Knoten die entsprechenden Werte verschieden, so folgt, daß diese Knoten nicht äquivalent sind, insbesondere der eine nicht in den anderen verformt werden kann. Umgekehrt kann man jedoch aus der Übereinstimmung der Werte i. allg. nicht schließen, daß die beiden Knoten zueinander äquivalent sind!

Der wohl einfachste Zugang zur Knotentheorie ist kombinatorischer Art und kommt ohne umfangreiches Vorwissen aus. Man betrachtet speziell solche Knoten, die aus endlich vielen geradlinigen Strecken im drei-dimensionalen Raum bestehen. Geeignet in die Ebene projiziert wird ein derartiger Knoten durch ein Diagramm dargestellt (Abb. 1). Bei zwei sich in der Projektion kreuzenden Strecken wird durch eine Unterbrechung der einen Strecke angegeben, daß diese Strecke im Knoten unterhalb der anderen verlaufen soll.

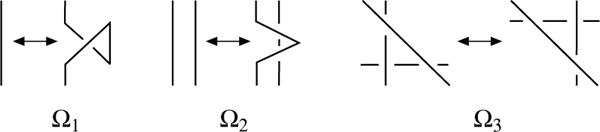
Kompliziertere Kreuzungsarten können vermieden werden und werden nicht zugelassen. So kann man den Knoten aus dem Diagramm im wesentlichen rekonstruieren, ihn also bis auf Äquivalenz durch das Diagramm vollständig angeben. Die Äquivalenz von Knoten läßt sich nun an Hand der Diagramme – abgesehen von Verformungen der Ebene – durch eine endliche Serie von drei Arten Ω₁, Ω₂, Ω₃ von Reidemeisterbewegungen (nach K.Reidemeister) beschreiben, bei denen das jeweilige Diagramm nur in einem bestimmten Bereich verändert wird (wie in Abb. 2 angedeutet) und sonst überall erhalten bleibt [1, 3, 5, 7, 8].

Wie man mit einer Knoteninvariante arbeitet, läßt sich nun am Beispiel erklären. Ein Diagramm eines Knotens wird dreifarbig genannt, wenn seine ununterbrochenen Streckenzüge so mit genau drei Farben versehen werden können, daß in der Nähe jeder Kreuzung die Zahl der vorkommenden Farben eins oder drei ist [1, 5, 8]. Das Diagramm der Kleeblattschlinge in Abb. 3 ist „dreifarbig“, wobei die Farben hier durch unterschiedliche Strichführungen angedeutet werden.

Das Diagramm □ ohne Keuzungen, das einen sog. trivialen Knoten darstellt, ist nicht dreifarbig, weil es nicht möglich ist, beim Färben mehr als eine Farbe zu verwenden. Entscheidend ist nun, daß bei den Reidemeisterbewegungen die Dreifarbigkeit erhalten bleibt [1]. Für einen gegebenen Knoten sind also alle Diagramme dreifarbig oder keines ist dreifarbig. Die sich ergebende Knoteninvariante ist „dreifarbig, ja oder nein“. Die Kleeblattschlinge ist dreifarbig, der triviale Knoten nicht. Damit ist bewiesen, daß diese beiden Knoten nicht zueinander äquivalent sind. Insbesondere kann man die Kleeblattschlinge nicht in einen trivialen Knoten verformen, sie ist „nichttrivial“.

Mit der Summe zweier Knoten, die dem Hintereinanderknüpfen zweier Knoten auf einer Schnur entspricht, erhält die Menge der Äquivalenzklassen aller Knoten die Struktur einer kommutativen Halbgruppe, in der jedes Element eine eindeutige Zerlegung in Primelemente, die Primknoten, gestattet (H.Schubert). Ein nichttrivialer Knoten hat darin kein inverses Element, was die Erfahrung bestätigt, daß man einen Knoten nicht dadurch auflösen kann, daß man einen weiteren hinzufügt. In einer Knotentabelle werden endlich viele der abzählbar unendlich vielen existierenden verschiedenen, nicht äquivalenten Primknoten nach minimaler Kreuzungszahl ihrer Diagramme (auch eine Knoteninvariante!) geordnet aufgeführt. Eine solche Tabelle zu erstellen, hat schon P.G. Tait im 19. Jahrhundert begonnen, bevor sich die Topologie als Teilgebiet der Mathematik etabliert hatte [2, 4]. Damals erhoffte man sich vergeblich Einblick in die Physik der Atome durch Knoten als mathematische Modelle. In heutiger Zeit treten bei Grundfragen der theoretischen Physik neue, tiefere Beziehungen zur Knotentheorie auf.

Knoten- und Äquivalenzbegriff werden oft anders gefaßt als oben angegeben. Statt in ℝ³ betrachtet man auch Knoten in der 3-Sphäre S³, statt Streckenzügen auch differenzierbare geschlossene Kurven, weiter Diffeomorphismen an Stelle von Homöomorphismen zur Definition der Äquivalenz. Es ist aber bekannt, daß sich die Klassifikationsaufgabe durch diese Begriffsabwandlung nicht ändert. Betrachtet man mehrere geschlossene Kurven gleichzeitig, spricht man von einer Verkettung oder Verschlingung (engl. link). Man kann diese auch mit einer Orientierung (hier: Durchlaufungsrichtung) versehen und verlangen, daß diese bei Äquivalenz erhalten bleibt. Die einfachste Invariante ist hier die Verschlingungszahl von zwei disjunkten geschlossenen Kurven. Sie wurde schon von C.F. Gauß zu Beginn des 19. Jahrhunderts bei astronomischen Studien betrachtet, wobei die Kurven die Bahnen von Himmelskörpern darstellten [4]. In der Chemie der Molekülketten (DNS, Polymere) dienen Knoten und Verkettungen als mathematische Modelle zur Beschreibung von Gestalt und Anordnung im Raum [10]. Hier spielt neben der Art der Verknotung auch eine Symmetrieeigenschaft eine bedeutende Rolle: Wenn ein Knoten zu seinem Spiegelbild äquivalent ist, heißt er achiral (oder amphicheiral), andernfalls chiral. Solche chiralen Molekülketten treten wirklich auf. Sie sind also zusammen mit ihrem Spiegelbild immer in zwei nicht äquivalenten Formen denkbar. Zahlreiche Invarianten geben hinreichende Kriterien für Chiralität, insbesondere die Signatur, die Knotengruppe samt peripherem System und das Jones-Polynom (s.u.). Beispielsweise ist die Signatur eines achiralen Knotens null. An deren Nichtverschwinden kann man also die Chiralität erkennen.

Die bis hier beschriebene kombinatorische Sichtweise gibt nur eine Facette der Knotentheorie wieder. Bedeutender und reichhaltiger ist die Knotentheorie als Teil der drei-dimensionalen Topologie und durch ihre Beziehungen zu anderen Gebieten der Mathematik. Taits mehr experimenteller Erforschung von Knoten stehen als Ursprung der systematischen Entwicklung der Knotentheorie W.Wirtingers Untersuchungen des Verzweigungsverhaltens algebraischer Funktionen zweier komplexer Variablen an singulären Stellen gegenüber. Sind p und q zwei teilerfremde ganze Zahlen ≥ 2, so ist die Nullstellenmenge der Funktion z₁^p + z₂^q in ℂ² nicht glatt, sie schneidet die drei-dimensionale Randsphäre S einer kleinen kugelförmigen Umgebung des Nullpunktes vielmehr in einem nichttrivialen Knoten in S, einem Torusknoten, der so heißt, weil er im Rand eines unverknoteten Volltorus untergebracht werden kann. Für p = 2, q = 3 z. B. ergibt sich die Kleeblattschlinge, allgemeiner treten iterierte Torusknoten und Verkettungen von solchen auf.

Eine für den topologischen Zugang zur Knotentheorie grundlegende Stellung nimmt die Knotengruppe ein, das ist die Fundamentalgruppe des Außenraumes eines Knotens, d. h. des Knotenkomplements. Sie läßt sich durch endlich viele Erzeugende und Relationen beschreiben (W. Wirtinger) und ist eine der ersten Knoteninvarianten. Sie ist genau dann unendlich zyklisch, wenn der Knoten trivial ist (M. Dehn, C. Papakyriakopoulos). Dies folgt aus dem berühmten Dehnschen Lemma, das erst nach langer Zeit vollständig bewiesen wurde. Ein nichttriviales Zentrum hat die Knotengruppe genau dann, wenn der Knoten ein Torusknoten ist (G. Burde und H. Zieschang). Zusammen mit dem peripheren System bestimmt sie die Äquivalenzklasse des Knotens eindeutig (F. Waldhausen). Vom Außenraum selbst ist bekannt, daß er im Fall eines Primknotens dessen Äquivalenzklasse bestimmt (C. Gordon und W. Luecke). In einen Knoten eingespannte orientierbare (d. h. zweiseitige) Flächen wurden zuerst von H.Seifert systematisch konstruiert und zur Untersuchung von Knoten herangezogen. Das kleinste Geschlecht dieser Flächen ist das Geschlecht des Knotens. Es verhält sich additiv zur Summe von Knoten, weshalb Knoten vom Geschlecht Eins Primknoten sind. Seifertflächen ermöglichen über die Seifertmatrizen auch die Berechnung der Homologieinvarianten der zyklischen Überlagerungen des Außenraumes, darunter des Alexander-Polynoms, der Signatur und der Arf-Invariante. Schließlich führte das Studium von Seifertflächen auf einen Algorithmus zur Klassifikation aller Knoten (W. Haken, F. Waldhausen, G. Hemion). Die Bedeutung der Knotentheorie innerhalb der drei-dimensionalen Topologie wird auch durch das Resultat von J.W. Alexander unterstrichen, daß jede kompakte orientierbare zusammenhängende unberandete Mannigfaltigkeit der Dimension drei homöomorph zu einer verzweigten Überlagerung eines Knotens oder einer Verkettung in der 3-Sphäre ist. Mit Hilfe der sog. Dehn-Chirurgie (engl. surgery) wird gezeigt, daß jede derartige Mannigfaltigkeit außerdem konstruiert werden kann, indem eine Umgebung einer Verkettung in der 3-Sphäre herausgenommen und anders wieder „eingeklebt“ wird. Wann dabei für verschiedene Verkettungen die gleiche Mannigfaltigkeit entsteht, ist von R. Kirby genau beschrieben worden. Über die „Property P“ genannte Eigenschaft von Knoten besteht hier ein enger Zusammenhang mit der alten, bis jetzt ungeklärten Poincaré-Vermutung, die besagt, daß jede einfach zusammenhängende Mannigfaltigkeit der o. g. Art homöomorph zur 3-Sphäre ist.

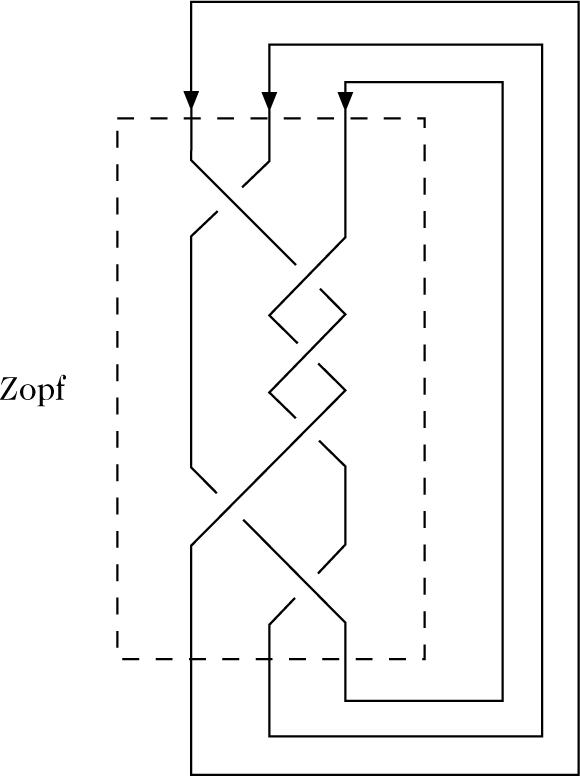
Der Begriff des Zopfes – ähnlich dem des Knotens unserer realen Welt entlehnt – spielt für die kombinatorische Knotentheorie eine zentrale Rolle. Ein mathematischer Zopf (engl. braid) besteht aus n disjunkten Kurven, den Strängen, die eine obere mit einer zu dieser parallelen unteren Ebene verbinden [1, 3, 5, 8]. Die Stränge beginnen oben in Punkten, die in einer Linie nebeneinander liegen, und enden in den entsprechenden Punkten unten. Abb. 4 zeigt dies schematisch bei horizontaler Blickrichtung. Beim Durchlaufen eines jeden Stranges von oben nach unten nimmt die Höhe streng monoton ab, so daß jeder Strang für sich unverknotet ist. Die verschiedenen Stränge dürfen aber miteinander verschlungen sein.

Es wird nicht gefordert, daß der oben vom k-ten Punkt ausgehende Strang unten im k-ten Punkt endet. Mit einer Äquivalenzrelation ähnlich wie bei Knoten und einer Verknüpfung von Zöpfen, die im Untereinandersetzen besteht, bilden die Zopfklassen mit n Strängen die Zopfgruppe \(\begin{eqnarray}{ {\mathcal B} }_{n}\end{eqnarray}\). Sie wurde von E. Artin eingeführt und durch Erzeugende σ₁,…,σ_n−1 und Relationen σ_iσ_k = σ_kσ_i (für |i − k| > 1) sowie σ_iσ_i+1σ_i = σ_i+1σ_iσ_i+1 (für i = 1,…,n − 2) beschrieben. Die zuletzt genannten Relationen entsprechen Reidemeisterbewegungen vom Typ Ω₃. \(\begin{eqnarray}{ {\mathcal B} }_{n}\end{eqnarray}\) läßt sich auch als Fundamentalgruppe eines bestimmten Konfigurationsraumes darstellen und tritt als Untergruppe der Automorphismengruppe der ( freien) Fundamentalgruppe des Komplements von n Punkten in der Ebene auf. Damit werden Zöpfe klassifiziert, und die Zopfgruppe erweist sich als torsionsfrei. Einen Zusammenhang zur Knotentheorie stellt man her, indem man die Endpunkte eines Zopfes außen herum durch in einer Ebene liegende Kurven mit den Anfangspunkten zum Zopfknoten bzw. zur Zopfverkettung verbindet, wobei eine Orientierung mitgeliefert wird (Abb. 4). Nach J.W. Alexander kann jeder Knoten und jede Verkettung auf diese Weise durch einen Zopf mit einer geeigneten Anzahl von Strängen realisiert werden. Ein wichtiger Satz von A.Markow gibt an, unter welchen Bedingungen zwei Zöpfe mit möglicherweise verschiedenen Anzahlen von Strängen zu äquivalenten Knoten oder Verkettungen führen. Die Minimalzahl der bei der Konstruktion benötigten Stränge ist der Zopfindex, eine Knoteninvariante. Man kann zeigen, daß diese gleich der Minimalzahl der Seifertkreise ist, die bei Seiferts Konstruktion einer eingespannten Fläche auftreten.

Es waren die Zopfgruppen und der Satz von Markow, die V. Jones Mitte der achtziger Jahre bei Untersuchungen über Operatoralgebren auf die Entdeckung eines neuen Laurentpolynoms (heute Jones-Polynom genannt) als Knoteninvariante führten. Ein Laurentpolynom ist hier ein ganzzahliges Polynom in einer oder mehreren Variablen, bei dem auch negative, u. U. auch halbzahlige, Exponenten vorkommen dürfen. Von dieser Neuerung gingen zahlreiche Impulse für die Entwicklung der Knotentheorie und ihre Anwendungen aus. Es wurden als wichtigste das HOMFLY-Polynom oder Homflypt-Polynom (nach den Anfangsbuchstaben der Namen seiner Entdecker benannt) und das Kauffman-Polynom (nach L.H. Kauffman) gefunden. Diese ebenso wie das ältere Alexander-Polynom, das auch topologisch gut interpretiert ist, können alle durch kombinatorische Diagrammrelationen (engl. skein relations) definiert und berechnet werden. Diese Relationen betreffen die Diagramme, die man erhält, wenn man das Kreuzungsverhalten an nur einem Kreuzungspunkt ändert. Für das Jones-Polynom V(L) einer Verkettung L lautet die Relation z. B. ([7]) \begin{eqnarray}{t}^{-1}V({L}_{+})-tV({L}_{-})=({t}^{1/2}-{t}^{-1/2})V({L}_{0}),\end{eqnarray} wobei sich die Diagramme von L₊, L₋ und L₀ nur in einem Kreuzungspunkt unterscheiden, und zwar in der in Abb. 5 angegebenen Weise.

Zusammen mit der Bedingung, daß der triviale Knoten das Jones-Polynom V = 1 hat, charakterisiert die Diagrammrelation sogar das Jones-Polynom, und man kann diese Knoteninvariante damit für jede orientierte Verkettung prinzipiell berechnen. Im Gegensatz zum Alexander-Polynom erlaubt das Jones-Polynom häufig, die Chiralität einer Verkettung zu beweisen; z. B. trifft das für die Kleeblattschlinge zu. Ob ein nichttrivialer Knoten mit trivialem Jones-Polynom existiert, ist eine interessante, bislang unbeantwortete Frage. Als weitere Anwendung der neuen Polynominvarianten ergibt sich ein Beweis der alten drei Tait-Vermutungen [9]. Deren Aussagen betreffen alternierende Verkettungen. Das sind solche, die ein Diagramm gestatten, bei dem sich im Durchlaufen überkreuzende und unterkreuzende Strecken abwechseln (wie z. B. in Abb. 1). Ein derartiges Diagramm realisiert nun nach einer der Tait-Vermutungen die minimale Kreuzungszahl der Verkettung, sofern es reduziert ist; diese letztere Bedingung besagt, daß keine geschlossene doppelpunktfreie Kurve existiert, die das Diagramm nur in einem Kreuzungspunkt trifft und dabei in zwei Teile zerlegt.

Über die Anwendungen innerhalb der Knotentheorie hinaus schufen die Knotenpolynome durch ihren kombinatorischen Aspekt Beziehungen zur Darstellungstheorie und zur statistischen Mechanik [5]. Hinzunahme der Relationen \({\sigma }_{i}^{2}=1\) macht aus der Artinschen Zopfgruppe \(\begin{eqnarray}{ {\mathcal B} }_{n}\end{eqnarray}\) die Permutationsgruppe \(\begin{eqnarray}{ {\mathcal S} }_{n}\end{eqnarray}\): Die einem Zopf entsprechende Permutation wird dadurch bestimmt, an welcher Platznummer jeweils der oben am i−ten Platz beginnende Strang unten endet. Deformation der entsprechenden Darstellung von \(\begin{eqnarray}{ {\mathcal B} }_{n}\end{eqnarray}\) in die Gruppenalgebra führt zu einer Hecke-Algebra und über eine geeignete Spur zu einer Knoteninvariante, die nach einer Variablentransformation ein Laurentpolynom in zwei Variablen ist und eine kombinatorische Diagrammrelation erfüllt, nämlich zum o. g. Homflypt-Polynom, das sich zum Jones-Polynom spezialisieren läßt. Eine Darstellung einer Zopfgruppe in eine Temperley-Lieb-Algebra konstruierte Kauffman über sein Klammerpolynom. Hier begegnet man der Yang-Baxter-Gleichung der statistischen Mechanik, die als Bedingung für die Invarianz unter der Reidemeisterbewegung Ω₃ auftaucht.

Umgekehrt liefert der Kalkül der statistischen Mechanik über die Kombinatorik der Diagrammrelationen jeweils Polynominvarianten für Verkettungen. Im Rahmen der Theorie der Quantengruppen werden Invarianten von Verkettungen mit trivialisierten Normalenbündeln (engl. framed links) konstruiert (N.Y. Reshetikhin, V.G. Turaev). Die Äquivalenzrelation für diese Objekte ist die reguläre Isotopie, die von den Reidemeisterbewegungen Ω₂ und Ω₃ erzeugt wird. Der Baustein einer Zerlegung einer Verkettung ist hier das Gewirr (engl. tangle), d. i. ein System von in einem kompakten Würfel D gelegenen disjunkten Kurven, deren Endpunkte gegebenenfalls im Rand von D liegen. Eine Verbindung zwischen diesem Zweig der Knotentheorie und der Quantenfeldtheorie der Physik besteht über die von E.Witten angegebenen, durch die nichtabelsche Eichtheorie (engl. gauge theory) inspirierten Quanteninvarianten für dreidimensionale Mannigfaltigkeiten, die man aus Verkettungen durch Dehn-Chirurgie konstruiert [2].

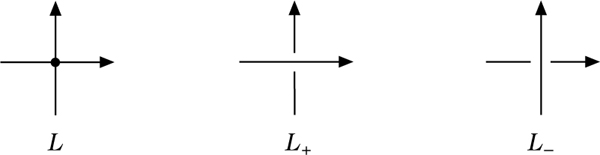
Neue Knoteninvarianten entstammen auch dem Studium des Raumes der Abbildungen des Kreises in den ℝ³ durch V.A. Vassiliev. Eine Knoteninvariante v kann man auf singuläre Knoten, d. s. Immersionen mit endlich vielen transversalen Doppelpunkten, erweitern, indem man induktiv definiert: v(L) := v(L₊) − v(L₋). Dabei entstehen L₊ und L₋ aus L durch Ersetzen eines Doppelpunktes durch die beiden Kreuzungsmöglichkeiten in einem Diagramm gemäß Abb. 6.

Vassiliev-Invarianten vom Typ n sind solche, die auf singulären Knoten mit mehr als n Doppelpunkten verschwinden [9]. Nach geeigneter Transformation der Variablen sind die Koeffizienten der Knotenpolynome sowie der Reshetikhin-Turaev-Invarianten von endlichem Typ (D. Bar-Natan, J. Birman, X.S. Lin). Das gleiche gilt für die Arf-Invariante, nicht jedoch für die minimale Kreuzungszahl, die Signatur, das Geschlecht und den Zopfindex. Im Rahmen von Sehnendiagrammen (engl. chord diagrams) versucht man, sich eine Übersicht darüber zu verschaffen, wieviele Vassiliev-Invarianten es gibt und welchen Informationsgehalt sie haben [6].

Knoten haben Analoga in höheren Dimensionen. Man betrachtet zu Sⁿ homöomorphe, lokal glatt in S^m eingebettete Mannigfaltigkeiten in der topologischen, stückweise linearen (=p.l.) oder differenzierbaren Kategorie, mit den entsprechenden Äquivalenzbegriffen. Für m − n ≥ 3 sind alle Knoten in der topologischen und in der stückweise linearen Kategorie äquivalent (J. Stallings, E.C. Zeeman). Falls der Knoten zu Sⁿ diffeomorph ist, gilt das in der differenzierbaren Kategorie für \(m\gt\frac{3}{2}(n+1)\), nicht aber für m = 6k, n = 4k − 1 (A.Haefliger). Der allgemeine Fall der Kodimension m − n = 2 weist viele Züge der klassischen Knotentheorie (n = 1) auf: Man hat eine aussagekräftige Knotengruppe, man kann Seiferthyperflächen in den Knoten einspannen, man hat Seifertmatrizen, die gegebenenfalls Invarianten von zyklischen Überlagerungen bestimmen, wie das Alexander-Polynom, die Signatur und die Arf-Invariante. Für n ≥ 5 folgt aus „topologisch unverknotet“ bereits „differenzierbar unverknotet“ (J. Levine). Es kommen exotische Sphären, d. h. zu Sⁿ homöomorphe, aber nicht diffeomorphe Mannigfaltigkeiten, in Sⁿ⁺² vor (M. Kervaire, J. Milnor), sogar als Ränder der Umgebungen von Singularitäten der Nullstellengebilde von Polynomen in komplexen Variablen (E. Brieskorn). Die differenzierbare Struktur der eingebetteten Sphäre ist eine topologische Invariante (durch Signatur bzw. Arf-Invariante gegeben). Die Menge der Äquivalenzklassen trägt eine kommutative Halbgruppenstruktur, aber es gilt i. allg. keine eindeutige Zerlegbarkeit in Primelemente (E. Bayer, C. Kearton). Die Kobordismus-relation macht diese Halbgruppe im differenzierbaren Fall zur Gruppe: Zwei Knoten K₁ und K₂ in Sⁿ⁺² heißen kobordant, wenn in Sⁿ⁺² × [0, 1] eine zu Sⁿ × [0, 1] diffeomorphe Untermannigfaltigkeit existiert, die Sⁿ⁺² × {0} bzw. Sⁿ⁺² × {1} genau in K₁ × {0} bzw. K₂ × {1} transversal schneidet. Signatur und Arf-Invariante sind Kobordismusinvarianten. Für gerades n ist die Kobordismusgruppe trivial (M. Kervaire). Für ungerades n ≥ 5 wurde ihre Berechnung von J. Levine mit Hilfe von Seifertmatrizen auf rein algebraische Fragen bzgl. quadratischer Formen zurückgeführt. Sie ist eine direkte Summe von zyklischen Gruppen der Ordnungen 2, 4, ∞, wobei von jeder dieser Gruppen unendlich viele als direkte Summanden auftreten. In der klassischen Knotentheorie erhält man auf diese Weise keine vollständige Beschreibung der Kobordismusgruppe (A. Casson und C. Gordon). – Inwieweit die mehr kombinatorische Seite der drei-dimensionalen Knotentheorie in der höherdimensionalen ihr Gegenstück hat, ist bis jetzt nicht klar.

Die Knotentheorie ist sicher kein Teilgebiet der Mathematik mit feststehenden Begriffen und Methoden. Sie führt vielmehr ein offenes Dasein und lebt auch von immer neuen, sich manchmal unerwartet auftuenden Querverbindungen zwischen Phänomenen ganz verschiedener Herkunft, in jedem Fall eine für die Mathematik typische Erscheinung.

[4] Epple, M.: Die Entstehung der Knotentheorie. Vieweg Braunschweig/Wiesbaden, 1999.

[5] Kauffman, L.H.: Knoten. Spektrum Akademischer Verlag Heidelberg, 1995.

[6] Kawauchi, A.: A Survey of Knot Theory. Birkhäuser Basel, 1996.

[7] Lickorish, W.B.R.: An Introduction to Knot Theory. Springer New York, 1997.

[8] Livingston, C.: Knotentheorie für Einsteiger. Vieweg Braunschweig/Wiesbaden, 1995.

[9] Murasugi, K.: Knot Theory and Its Applications. Birkhäuser Boston, 1996.

[10] Sumners, D.W.L. ed.: New Scientific Applications of Geometry and Topology. American Mathematical Society Providence, R.I., 1992.