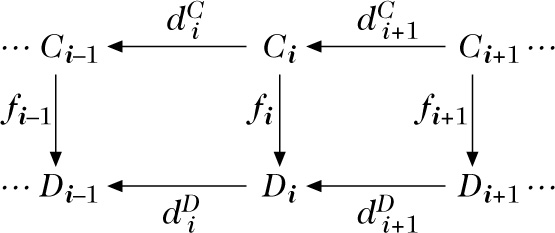
üblicherweise bezeichnet mit f : C_• → D_•, eine Folge von Abbildungen f_i : C_i → D_i (i ∈ ℤ) zwischen den Objekten zweier Komplexe \(C\bullet =({C}_{i},{d}_{i}^{C})\) und \(D\bullet =({D}_{i},{d}_{i}^{D})\) abelscher Gruppen, Vektorräume, R-Module oder allgemeiner abelscher Kategorien, die die Bedingung \begin{eqnarray}{d}_{i}^{D}\circ {f}_{i}={f}_{i-1}\circ {d}_{i}^{C},\ \ i\in {\mathbb{Z}}\end{eqnarray}

erfüllen.

Ein Komplexmorphismus f induziert eine Familie von natürlichen Abbildungen \begin{eqnarray}{\bar{f}}_{n}:{H}_{n}(C\bullet )\to {H}_{n}(D\bullet )\end{eqnarray}

Die (Ko)Komplexe bilden mit den Komplexmorphismen eine abelsche Kategorie.