Lösung der konfluenten hypergeometrischen Differential-gleichung in z, \begin{eqnarray}z\frac{{d}^{2}w}{d{z}^{2}}+(c-z)\frac{dw}{dz}-aw=0\end{eqnarray}

mit a, c ∈ ℂ. Eine Lösung dieser Differentialgleichung ist durch die Kummer-Funktion M(a, c, z) gegeben: \begin{eqnarray}\begin{array}{cc}M(a,c,z):=\displaystyle \sum _{s=0}^{\infty }\frac{{(a)}_{s}{z}^{s}}{{(c)}_{s}s!} & (c\notin {\mathbb{Z}}).\end{array}\end{eqnarray}

Dabei ist (a)_n das Pochhammer-Symbol, definiert durch \begin{eqnarray}\begin{array}{lll}{(a)}_{n} & := & a\cdot (a+1)(a+2)\cdots (a+n-1)\\ {(a)}_{0} & := & 1.\end{array}\end{eqnarray}

Andere Notationen für die Kummer-Funktion sind Φ(a, c; z) oder auch ₁F₁(a, c; z). Letzteres ist die Kummer-Funktion in der Notation der verallgemeinerten hypergeometrischen Funktionen.

Die Kummer-Funktion ist eine ganze Funktion in z, und für festes z auch ganz in a. Betrachtet man M(a, ·, z) als Funktion von c, so erhält man eine meromorphe Funktion mit möglichen Polen bei −c ∈ ℕ₀; hingegen ist M(a, c,z)Γ(c) wiederum ganz in c.

Für c / ∈ ℤ ist eine weitere linear unabhängige Lö-sung der hypergeometrischen Differentialgleichung gegeben durch \begin{eqnarray}N(a,c,z):={z}^{1-c}M(1+a-c,2-c,z).\end{eqnarray}

Weiterhin ist noch die folgende Linearkombination beider Lösungen gebräuchlich \begin{eqnarray}\begin{array}{lll}U(a,c,z) & := & \frac{\pi }{\sin \pi c}\\ & & \left(\frac{M(a,c,z)}{\Gamma (c)\Gamma (1+a-c)}-\frac{N(a,c,z)}{\Gamma (2-c)\Gamma (c)}\right),\end{array}\end{eqnarray}

sowie die Abkürzungen \begin{eqnarray}\begin{array}{lll}M(a,c,z) & := & \frac{M(a,c,z)}{\Gamma (c)},\\ N(a,c,z) & := & \frac{N(a,c,z)}{\Gamma (2-c)}.\end{array}\end{eqnarray}

Die folgenden acht Lösungen der konfluenten hypergeometrischen Differentialgleichung fassen die gebräuchlichsten hypergeometrischen Funktionen zusammen: \begin{eqnarray}\begin{array}{lll}{y}_{1}(z) & = & M(a,c,z)\\ {y}_{2}(z) & = & {z}^{1-c}M(1+a-c,2-c,z)=N(a,c,z)\\ {y}_{3}(z) & = & {e}^{z}M(c-a,c,-z)\\ {y}_{4}(z) & = & {z}^{1-c}{e}^{z}M(1-a,2-c,-z)\\ {y}_{5}(z) & = & U(a,c,z)\\ {y}_{6}(z) & = & {z}^{1-c}U(1+a-c,2-c,z)\\ {y}_{7}(z) & = & {e}^{z}U(c-a,c,-z)\\ {y}_{8}(z) & = & {z}^{1-c}{e}^{z}U(1-a,2-c,-z)\end{array}\end{eqnarray}

Um festzustellen, welche der Lösungen linear unabhängig sind, benötigt man die folgenden WronskiDeterminanten: \begin{eqnarray}\begin{array}{lll}W({y}_{1}(z),{y}_{2}(z)) & = & W({y}_{3}(z),{y}_{4}(z))\\ & = & W({y}_{1}(z),{y}_{2}(z))\\ & = & W({y}_{3}(z),{y}_{2}(z))\\ & = & (1-c){z}^{-c}{e}^{z}\\ W({y}_{1}(z),{y}_{3}(z)) & = & W({y}_{2}(z),{y}_{4}(z))\\ & = & W({y}_{5}(z),{y}_{6}(z))\\ & = & W({y}_{7}(z),{y}_{8}(z))\\ & = & 0\\ W({y}_{1}(z),{y}_{5}(z)) & = & -\frac{\Gamma (c)}{\Gamma (a)}{z}^{-c}{e}^{z}\\ W({y}_{1}(z),{y}_{7}(z)) & = & {e}^{\varepsilon \pi ic}\frac{\Gamma (c)}{\Gamma (c-a)}{z}^{-c}{e}^{z}\\ W({y}_{2}(z),{y}_{5}(z)) & = & -\frac{\Gamma (2-c)}{\Gamma (1+a-c)}{z}^{-c}{e}^{z}\\ W({y}_{2}(z),{y}_{7}(z)) & = & -\frac{\Gamma (2-c)}{\Gamma (1-a)}{z}^{-c}{e}^{z}\\ W({y}_{5}(z),{y}_{7}(z)) & = & {e}^{\varepsilon \pi i(c-a)}{z}^{-c}{e}^{z}\\ & & \end{array}\end{eqnarray}

Dabei ist ϵ = 1 für Im z > 0 und ϵ = −1 für Im z ≤ 0.

Eliminiert man den Term erster Ordnung aus der konfluenten hypergeometrischen Differential-gleichung, so entsteht die Whittaker-Differential-gleichung \begin{eqnarray}\frac{{d}^{2}w}{d{z}^{2}}=\left(\frac{1}{4}-\frac{k}{z}+\frac{{m}^{2}-1/4}{{z}^{2}}\right)w\end{eqnarray}

mit den Standard-Lösungen \begin{eqnarray}{M}_{k,m}(z):={e}^{-z/2}{z}^{m+1/2}M(m-k+1/2,2m+1,z)\end{eqnarray}

und \begin{eqnarray}{M}_{k,m}(z):={e}^{-z/2}{z}^{m+1/2}U(m-k+1/2,2m+1,z),\end{eqnarray}

den sog. Whittaker-Funktionen. Beides sind mehrdeutige Funktionen mit je einem Verzweigungspunkt am Ursprung; den Hauptzweig dieser Funk-tionen definiert man dann durch Aufschneiden der komplexen Ebene längst der negativen reellen Achse.

Die folgenden Kummer-Transformationen verknüpfen die Lösungen zu verschiedenen Argumenten a und c miteinander: \begin{eqnarray}\begin{array}{rll}M(a,c,z) & = & {e}^{z}M(c-a,c,-z),\\ {z}^{1-c}M(1+a-c,2-c,z) & = & {z}^{1-c}{e}^{z}\\ & & M(1-a,2-c,-z),\\ U(a,c,z) & = & {z}^{1-c}\\ & & U(1+a-c,2-c,z),\\ {e}^{z}U(c-a,c,-z) & = & {e}^{\varepsilon \pi i(1-c)}{e}^{z}{z}^{1-c}\\ & & U(1-a,2-c,-z).\end{array}\end{eqnarray}

Diese Funktionen sind im Falle Re c > Re a > 0 auch durch Integrale darstellbar, hier eine Aus-wahl: \begin{eqnarray}\begin{array}{l}\begin{array}{l}\frac{\Gamma (c-a)\Gamma (a)}{\Gamma (b)}M(a,c,z)=\\ =\displaystyle \underset{0}{\overset{1}{\int }}{e}^{zt}{t}^{a-1}{(1-t)}^{c-a-1}dt,\end{array}\\ \Gamma (a)U(a,c,z)=\\ =\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-zt}{t}^{a-1}{(1+t)}^{c-a-1}dt.\end{array}\end{eqnarray}

Es gibt eine ganze Reihe von Rekursionsrelationen für die Kummerfunktion. Hier wieder nur eine kleine Auswahl, eine vollständigere Liste findet sich in der Literatur, z. B. [1]: \begin{eqnarray}\begin{array}{c}(c-a)M(a-1,c,z)+(2a-c+z)M(a,c,z)\\ -aM(a+1,c,z)=0,\\ c(c-1)M(a,c-1,z)+c(1-c-z)M(a,b,z)\\ +z(c-a)M(a,c+1,z)=0,\\ U(a-1,c,z)+(c-2a-z)U(a,c,z)\\ +a(1+a-c)U(a+1,c,z)=0,\\ (c-a-1)U(a,c-1,z)+(1-c-z)U(a,c,z)\\ +zU(a,c+1,z)=0\\ U(a,c,z)-aU(a+1,c,z)\\ -U(a,c-1,z)=0,\end{array}\end{eqnarray}

sowie Relationen zwischen M und seinen Ableitungen nach z: \begin{eqnarray}\begin{array}{lll}\frac{{d}^{n}}{d{z}^{n}}M(a,c,z) & = & \frac{{(a)}_{n}}{{(c)}_{n}}M(a+n,c+n,z),\\ \frac{{d}^{n}}{d{z}^{n}}U(a,c,z) & = & {(-1)}^{n}{(a)}_{n}U(a+n,c+n,z).\end{array}\end{eqnarray}

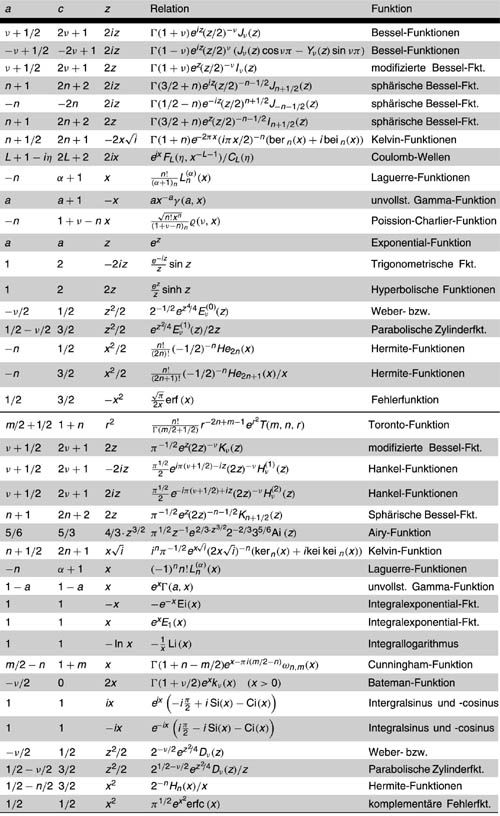
Einige Relationen der Kummer-Funktionen zu anderen speziellen Funktionen zeigt die Tabelle.

[1] Abramowitz, M.; Stegun, I.A.: Handbook of Mathematical Functions. Dover Publications, 1972.
[2] Buchholz, H.: Die konfluente hypergeometrische Funktion. Springer-Verlag Berlin/Heidelberg, 1953.
[3] Olver, F.W.J.: Asymptotics and Special Functions. Academic Press, 1974.