die Menge der reellen oder komplexen Zahlen, für die eine gegebene Potenzreihe \begin{eqnarray}\displaystyle \sum _{n=0}^{\infty }{a}_{n}{(x-{x}_{0})}^{n}\end{eqnarray}

konvergiert. Es seien dabei (a_n) (die Koeffizienten) eine Folge reeller oder komplexer Zahlen, und der Entwicklungspunkt x₀ ∈ 𝕂 mit 𝕂 ∈ {ℝ, ℂ}. Es gilt:

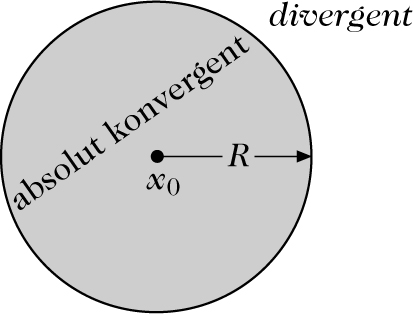
Entweder ist die o. a. Potenzreihe für alle x ∈ 𝕂 absolut konvergent, die Reihe wird dann auch beständig konvergent genannt, oder es existiert ein 0 ≤ R < ∞ derart, daß sie für x ∈ 𝕂 mit |x − x₀| < R absolut konvergent und für x ∈ 𝕂 mit |x − x₀| > R divergent ist.

Für positives (endliches) R ist dies in der Abbildung illustriert.

Setzt man im ersten Fall formal R := ∞ und ergänzt die Anordnung auf ℝ (bei sinngemäßer Übertragung aller damit gebildeten Notierungsweisen) durch −∞ < α < ∞ für α ∈ ℝ, dann läßt sich der Satz wie folgt umformulieren:

Es existiert ein 0 ≤ R ≤ ∞ derart, daß die o. a. Potenzreihe für x ∈ 𝕂 mit |x − x₀| < R absolut konvergent und für x ∈ 𝕂 mit |x − x₀| > R divergent ist.

Kennt man den Konvergenzradius, so überschaut man also den Konvergenzbereich einer Potenzreihe weitgehend. Die einzigen Punkte, in denen keine allgemeinen Aussagen über das Konvergenzverhalten gemacht werden können, sind – falls 0 < R < ∞ – die „Randpunkte“, für 𝕂 = ℝ also gerade x₀ − R und x₀ + R. Tatsächlich treten dort alle möglichen Fälle ein: Die Potenzreihen um 0 \begin{eqnarray}\begin{array}{cccc}\displaystyle \sum _{n=1}^{\infty }{x}^{n}, & \displaystyle \sum _{n=1}^{\infty }\frac{1}{n}{x}^{n}, & \displaystyle \sum _{n=1}^{\infty }{(-1)}^{n}\frac{1}{n}{x}^{n}, & \displaystyle \sum _{n=1}^{\infty }\frac{1}{{n}^{2}}{x}^{n}\end{array}\end{eqnarray}

haben alle den Konvergenzradius 1; sie sind in dieser Reihenfolge konvergent in (−1, 1), [−1, 1), (− 1, 1] und [−1, 1].

Der Bereich {x ∈ 𝕂 : |x − x₀| < R}, in dem die Konvergenz also stets gesichert ist, heißt Konvergenzintervall für 𝕂 = ℝ und Konvergenzkreis für 𝕂 = ℂ. Im Fall 𝕂 = ℂ sind alle Punkte auf dem „Rand“ des Konvergenzkreises gesondert zu untersuchen.

Für 0 < r < R ist die Potenzreihe in {x ∈ 𝕂 : | x−x₀| ≤ r} gleichmäßig absolut konvergent. Siehe auch Konvergenzkreis, Konvergenzradius.