Lexikon der Mathematik: konvexe Funktion
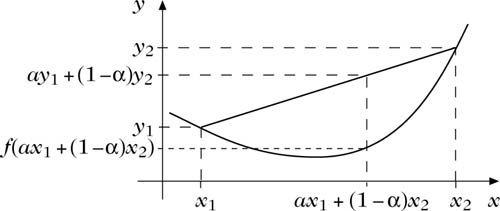
auf einem Intervall I ⊂ ℝ (oder auch allgemeiner einer konvexen Menge I) definierte Funktion f : I → ℝ mit der Eigenschaft
für alle x1, x2 ∈ I mit x1 ≠ x2 und α ∈ (0, 1). Dazu äquivalent ist die Jensen-Ungleichung
<?PageNum _195
für alle n ≥ 2, α1, …, αn ∈ (0, 1) mit \(\displaystyle {\sum }_{i=1}^{n}{\alpha }_{i}=1\) und paarweise verschiedene x1, …, xn ∈ I. Eine weitere äquivalente Bedingung ist
für alle x1, x2, x3 ∈ I mit x1< x2< x3, was man mit den DifferenzenquotientenQf (xi, xj) als
schreiben kann. Somit ist f genau dann konvex, wenn für jedes c ∈ I die Funktion
isoton ist.
Gilt in (1) oder, wieder äquivalent dazu, in (2) oder (3) sogar, <‘ so nennt man f streng konvex oder auch strikt konvex. Genau dann ist f streng konvex, wenn für jedes c ∈ I die Funktion Qf,c : I \{c} → ℝ streng isoton ist. Die Funktion f heißt (streng) konkav genau dann, wenn −f (streng) konvex ist. Anschaulich bedeutet Konvexität bzw. Konkavität, daß der Graph von f stets unterhalb bzw. oberhalb der Verbindungsstrecke je zweier seiner Punkte liegt. Bei differenzierbarem f bedeutet Konvexität bzw. Konkavität, daß alle Tangenten an f unterhalb bzw. oberhalb des Graphen von f liegen. Da Konvexität bzw. Konkavität sich anschaulich auch als, Linksgekrümmtheit‘ bzw., Rechtsgekrümmtheit‘ des Graphen der Funktion deuten läßt, spricht man auch vom Krümmungsverhalten der Funktion.
Konvexe Funktion
Im folgenden sei I offen. Ist f konvex, so ist f stetig (sogar Lipschitz-stetig auf jedem abgeschlossenen Teilintervall) sowie links- und rechtsseitig differenzierbar mit f′− ≤ f′+ (Satz von Stolz). Ferner sind dann f′− und f′+ isoton und unterscheiden sich höchstens an abzählbar vielen Stellen, d. h. f ist höchstens an abzählbar vielen Stellen nicht differenzierbar.
Genau dann ist f konvex, wenn es eine isotone Funktion φ : I → ℝ gibt und ein a ∈ I mit
für x ∈ I. Ist f differenzierbar, so ist f genau dann (streng) konvex bzw. konkav, wenn f′ (streng) isoton bzw. antiton ist. Ist f zweimal differenzierbar, so ist f genau dann konvex bzw. konkav, wenn f′′ ≥ 0 bzw. f′′ ≤ 0 gilt. Gilt f′′ > 0 bzw. f′′< 0, so ist f streng konvex bzw. konkav. Die durch f(x) = x4 gegebene streng konvexe Funktion zeigt, daß diese letzten Bedingungen nicht notwendig sind. Es gibt sogar streng konvexe oder streng konkave Funktionen mit fast überall verschwindender zweiter Ableitung, etwa eine Stammfunktion einer streng monotonen stetigen Funktion mit fast überall verschwindender Ableitung.
Eine Stelle x ∈ I, an der sich das Konvexitätsverhalten von f von strenger Konvexität zu strenger Konkavität oder umgekehrt ändert, nennt man einen Wendepunkt von f.
Die Forderung (1) alleine für \(\alpha =\frac{1}{2}\) führt zum Begriff der Jensen-konvexen oder mittelpunktkonvexen Funktion. Jede konvexe Funktion ist somit mittelpunktkonvex. Jede stetige mittelpunktkonvexe Funktion ist konvex. Man beachte: Teilweise werden in älterer Literatur mittelpunktkonvexe Funktionen als „konvexe Funktionen“ bezeichnet.
Konvexität und Konkavität von Funktionen lassen sich, wie eingangs erwähnt, über die Forderung (1) allgemeiner auch für reellwertige, auf einer konvexen Teilmenge eines reellen Vektorraums definierte Funktionen erklären. Eine auf einer offenen konvexen Menge I ⊆ ℝ
gilt. In der Optimierung konvexer Funktionen auf konvexen Mengen ist es beispielsweise von entscheidender Bedeutung, daß jeder lokale Minimal-punkt schon globaler Minimalpunkt ist.
Die Untersuchung der Eigenschaften konvexer Funktionen ist ein Gegenstand der konvexen Analysis.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.