Verfahren der mathematischen Statistik zur Untersuchung der Korrelationen, d. h. der stochastischen Abhängigkeiten von zufälligen Merkmalen anhand von Stichproben bzw. Punktschätzungen der entsprechenden Korrelationskoeffizienten.

1. Korrelationsanalyse mittels des einfachen Korrelationskoeffizienten. Es sei (X, Y) ein zweidimensionaler zufälliger Vektor und (X₁, Y₁), …, (X_n, Y_n) eine mathematische Stichprobe von (X, Y). Der einfache Korrelationskoeffizient wird dabei durch den empirischen Korrelationskoeffizienten \(\hat{\varrho }\), auch als Pearsonscher oder Stichprobenkorrelationskoeffizient bezeichnet, geschätzt. Unter der Annahme, daß (X, Y) eine zweidimensionale Normalverteilung besitzt und X und Y unkorreliert sind, besitzt die Größe \begin{eqnarray}T=\sqrt{n-2}\frac{\hat{\varrho }}{\sqrt{1-{\hat{\varrho }}^{2}}}\end{eqnarray}

eine t−Verteilung mit n − 2 Freiheitsgraden. Damit läßt sich ein Korrelationstest zum Prüfen der Hypothesen \begin{eqnarray}\begin{array}{cc}{H}_{\text{o}}:\varrho =0 & \text{(}X\ \text{und}\ Y\ \text{sind unkorreliert) gegen}\ {H}_{\text{1}}\mathrm{:\; \varrho }\ne \text{0}\end{array}\end{eqnarray}

konstruieren; die Hypothese H_o wird akzeptiert, wenn |T| < t_n−2(1 − α) ist, andernfalls abgelehnt. Dabei ist t_n−2(1 − α) das (1 − α)-Quantil der t-Verteilung mit (n − 2) Freiheitsgraden. α ist der vorgegebene Fehler erster Art dieses Signifikanztests.

Zur Konstruktion eines (asymptotischen) Tests zum Prüfen der Hypothese H_o : ϱ = ϱ_o(0 < | ϱ_o | < 1), zur Konstruktion eines (asymptotischen) Konfidenzintervalls, sowie zur Konstruktion von Tests zum Prüfen der Gleichheit zweier einfacher Korrelationskoeffizienten wird die sogenannte Fishersche Z-Transformierte (Z-Transformation) herangezogen.

In der deskriptiven Statistik ist es häufig üblich, ohne jedes Testverfahren folgende Klassifikation vorzunehmen:

• Wenn \(|\hat{\varrho }|\lt 0.2\) dann X, Y unkorreliert.
• Wenn \(0.2\le |\hat{\varrho }|\lt 0.5\) dann X, Y schwach korreliert.
• Wenn \(0.5\le |\hat{\varrho }|\lt 0.8\) dann X, Y korreliert.
• Wenn \(0.8\le |\hat{\varrho }|\) dann X, Y stark korreliert.

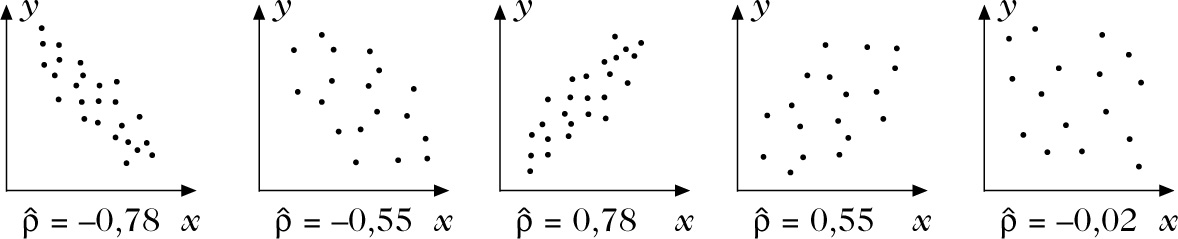
Man spricht von positiver Korrelation, wenn \(\hat{\varrho }\gt 0\), und von negativer Korrelation, wenn \(\hat{\varrho }\lt 0\). Da die einfache Korrelation den Grad der linearen Abhängigkeit zwischen den Zufallsgrößen widerspiegelt, gibt es einen typischen Zusammenhang zwischen der Gestalt der Stichprobenwerte als Punktwolke im kartesischen Koordinatensystem und dem Korrelationskoeffizienten \(\hat{\varrho }\), siehe Abbildung.

Ist wenigstens eines der beiden zufälligen Merkmale X und Y ordinal skaliert, so verwendet man zur Schätzung von ϱ einen Rangkorrelationskoef-fizienten, z. B. den Spearmanschen Korrelationskoeffizienten oder auch ein Assoziationsmaß wie Kendalls τ-Koefizient, und verwendet die parameterfreien Methoden der Rangkorrelationsanalyse zur Untersuchung des Zusammenhangs zwischen X und Y.

2. Korrelationsanalyse mittels der partiellen Korrelationskoeffizienten. Es sei \(\overrightarrow{X}=({X}_{1},\ldots,{X}_{m})\) ein zufälliger Vektor mit dem Erwartungswert \(E\overrightarrow{X}=\overrightarrow{\mu }\) und der Kovarianzmatrix B_x = B. Weiterhin bezeichne (X⁽¹⁾, X⁽²⁾) eine Zerlegung von X mit \begin{eqnarray}{X}^{(1)}=({X}_{1},\ldots,{X}_{p})\ \text{und}\ {X}^{(2)}=({X}_{p+1},\ldots,{X}_{m}),\ p\lt m,\end{eqnarray}

sowie \begin{eqnarray}\overrightarrow{\mu }=({\mu }^{(1)},{\mu }^{(2)})\ \text{bzw}.\ B=\left(\begin{array}{cc}{B}_{11} & {B}_{12}\\ {B}_{21} & {B}_{22}\end{array}\right).\end{eqnarray}

Sei \(\overrightarrow{X}=({X}_{i1},\ldots,{X}_{im})\), i =1, …, n eine zugehörige mathematische Stichprobe von \(\overrightarrow{X}\) vom Umfang n. Die Matrix \begin{eqnarray}\hat{B}={({\hat{b}}_{ij})}_{i,j=1,\ldots,m}=\left(\begin{array}{cc}{\hat{B}}_{11} & {\hat{B}}_{12}\\ {\hat{B}}_{21} & {\hat{B}}_{22}\end{array}\right)\end{eqnarray}

mit den Elementen \begin{eqnarray}{\hat{b}}_{ij}=\frac{1}{n-1}\displaystyle \sum _{k=1}^{n}({X}_{ki}-\bar{X}.i)({X}_{kj}-\bar{X}.j),\end{eqnarray}

wobei \begin{eqnarray}\bar{X}.i=\frac{1}{n}=\displaystyle \sum _{k=1}^{n}{X}_{ki}\end{eqnarray}

für i = 1, …, m, heißt Stichprobenkovarianzmatrix, die \(\hat{{b}_{ij}}\) Stichprobenkovarianzen und \(\hat{{b}_{ii}}\) die Stichprobenstreuungen. Für eine konkrete Stichprobe \({\overrightarrow{x}}_{i}=({x}_{i1},\ldots,{x}_{im})\), i =1, …, n, spricht man von der empirischen Kovarianzmatrix \(\hat{B}\), sowie den empirischen Kovarianzen und Varianzen \({\hat{b}}_{ij}\) und \({\hat{b}}_{ii}\).

Die Elemente \({\hat{\sigma }}_{ij.p+1,\ldots,m}\), i, j = 1, …, p der Matrix \(\hat{{B}_{11}}-{\hat{B}}_{12}{\hat{B}}_{22}^{-1}{\hat{B}}_{21}\) sind die ‚partiellen Stichprobenkovarianzen‘, und \begin{eqnarray}{\hat{\varrho }}_{ij.p+1,\ldots,m}=\frac{{\hat{\sigma }}_{ij.p+1,\ldots,m}}{\sqrt{{\hat{\sigma }}_{ii.p+1,\ldots,m}{\hat{\sigma }}_{jj.p+1,\ldots,m}}}\end{eqnarray} die partiellen Stichprobenkorrelationskoeffizienten; im Falle einer konkreten Stichprobe sprechen wir von den empirischen partiellen Kovarianzen und den empirischen partiellen Korrelationskoeffizienten. Ist \(\overrightarrow{X}\) normalverteilt, so stellt der partielle Stichprobenkorrelationskoeffizient \({\hat{\varrho }}_{ij.p+1,\ldots,m}\) die Maximum-Likelihood-Schätzung von ϱ_{ij·p+1, …, m} dar. Außerdem ist \begin{eqnarray}{T}_{ij}=\sqrt{n-(m-p)-2}\frac{{\hat{\varrho }}_{ij.p+1,\ldots,m}}{\sqrt{1-{\hat{\varrho }}_{ij.p+1,\ldots,m}^{2}}}\end{eqnarray}

(i, j = 1, …, p) im Falle ϱ_ij·p+1,…, m = 0 t-verteilt mit (n − (m − p) − 2) Freiheitsgraden. T_ij kann folglich als Testgröße zum Prüfen der Hypothese \begin{eqnarray}{H}_{o}:{e}_{ij.p+1,\ldots,m}=0\end{eqnarray}

verwendet werden.

Zum Prüfen der Hypothese \begin{eqnarray}{H}_{o}:{\varrho }_{ij.p+1,\ldots,m}={\varrho }_{0}\end{eqnarray}

ist eine Teststatistik auf der Basis der Fisher-schen Z-Transformation entwickelt worden. Für weitere sogenannte verteilungsfreie Methoden der Korreationsanalyse vergleiche man Rangkorrelationsanalyse.

3. Korrelationsanalyse mittels der multiplen Korrelationskoeffizienten. Ist in 2. p = 1, d. h., X⁽¹⁾ = (X₁) und X⁽²⁾ = (X₂, …, X_m), so ist \begin{eqnarray}{\hat{\varrho }}_{1(\mathrm{2\cdots }m)}=\sqrt{\frac{{\hat{\sigma }}_{1}{\hat{B}}_{22}^{-1}{\hat{\sigma }}_{1}^{T}}{\hat{{\sigma }_{11}}}}\end{eqnarray} mit \begin{eqnarray}{\hat{\sigma }}_{11}=\frac{1}{n-1}{\displaystyle \sum _{k=1}^{n}({X}_{k1}-\bar{X}{.}_{1})}^{2}\end{eqnarray} und \begin{eqnarray}{\hat{\sigma }}_{1}=\frac{1}{n-1}\displaystyle \sum _{k=1}^{n}({X}_{k1}-\bar{X}{.}_{1})({X}_{k}^{(2)}-{\bar{X}}_{.}^{(2)})\end{eqnarray} eine Punktschätzung für den multiplen Korrelationskoeffizienten ϱ_1(2···m).

Der Wert \({\hat{\varrho }}_{1(\mathrm{2\cdots}m)}\) heißt multipler Stichprobenkorrelationskoeffizient bzw., wenn er auf der Basis einer konkreten Stichprobe berechnet wird, empirischer multipler Korrelationskoeffizient. Falls \(\overrightarrow{X}\) normalverteilt ist, stellt \({\hat{\varrho }}_{1(\mathrm{2\cdots}m)}\) die Maximum-Likelihood-Schätzung von ϱ_1(2···m) dar, und \begin{eqnarray}T=\frac{n-m}{m-1}\left(\frac{{\hat{\varrho }}_{1(\mathrm{2\cdots}m)}^{2}}{1-{\hat{\varrho }}_{1(\mathrm{2\cdots}m)}^{2}}\right)\end{eqnarray}

ist F-verteilt mit (n − 1, n − m) Freiheitsgraden. T kann folglich zum Prüfen der Hypothese \begin{eqnarray}{H}_{o}:{\varrho }_{1(\mathrm{2\cdots}m)}=0\end{eqnarray}

herangezogen werden.

Für weitere sogenannte verteilungsfreie Methoden der Korreationsanalyse vergleiche man Rang-korrelationsanalyse.