Lexikon der Mathematik: Kreuzungszahl
minimale Anzahl von Kreuzungen in einer normalen Einbettung eines Graphen in die Ebene ℝ2.
Da jeder Graph eine solche Einbettung besitzt, ist die Kreuzungszahl wohldefiniert. Oft sind für die Kreuzungszahl spezieller Graphen nur obere Schranken bekannt, die durch Angabe einer konkreten Einbettung bewiesen werden.
Die Kreuzungszahl des vollständigen Graphen Kn beträgt so höchstens
und die Kreuzungszahl des vollständigen bipartiten Graphen Kn,m beträgt höchstens
Die Frage nach dem genauen Wert der Kreuzungszahl des vollständigen bipartiten Graphen ist als „Turán’s brick-factory problem“ bekannt.
Die oben angegebene Schranke wurde 1954 von K.Zarankiewicz bewiesen.
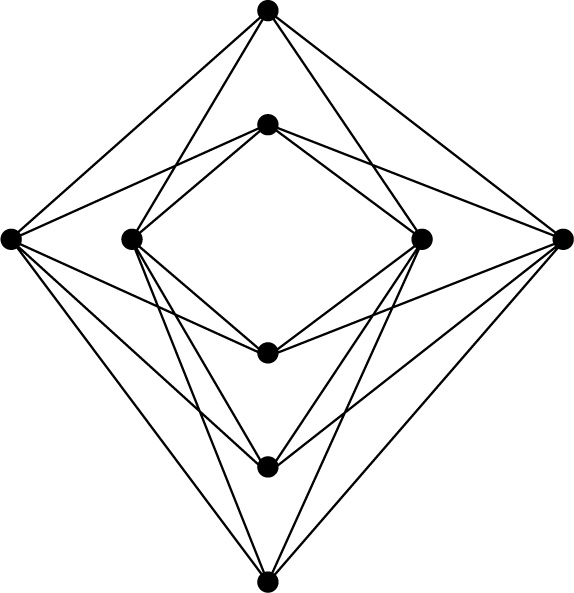
Eine normale Einbettung des vollständigen bipartiten Graphen K4,5 in die Ebene ℝ2 mit \(\lfloor \frac{4}{2}\rfloor \lfloor \frac{3}{2}\rfloor \lfloor \frac{5}{2}\rfloor \lfloor \frac{4}{2}\rfloor =8\) Kreuzungen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.