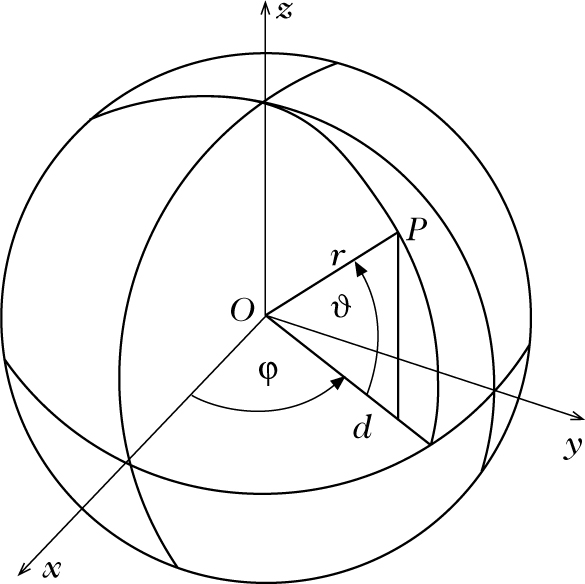
sphärische Koordinaten, das Tripel (r, ϑ, ϕ), bestehend aus dem Abstand r ≥ 0 eines Punkts P ∈ ℝ³ vom Ursprung O, dem Winkel \(\vartheta \in [-{\scriptstyle \frac{\pi }{2}},{\scriptstyle \frac{\pi }{2}}]\) zwischen der Strecke OP und der (x, y)-Ebene, und dem Winkel ϕ ∈ [0, 2π) (Azimut) zwischen der Projektion der Strecke OP in die (x, y)-Ebene und der x-Achse.

Man beachte: Oft wird statt dessen ϑ als Winkel zur z-Achse (Polwinkel oder Poldistanz) definiert. Dann sind in den unten folgenden Transformationsformeln sin ϑ und cos ϑ zu vertauschen, und die Richtung von e_ϑ ist umzudrehen.

Kugelkoordinaten sind ein wichtiges Beispiel für krummlinige Koordinaten. Variiert man ϑ und ϕ bei festem r, so beschreibt (r, ϑ, ϕ) die Oberfläche S_r der Kugel mit Mittelpunkt im Ursprung und Radius r. Variiert man r bei festen ϑ und ϕ, so beschreibt (r, ϑ, ϕ) eine Halbgerade durch O (Radialstrahl). Variiert man ϑ bei festen r und ϕ, so beschreibt (r, ϑ, ϕ) einen Längenhalbkreis oder Meridian bei der geographischen Länge ϕ auf S_r. Variiert man ϕ bei festen r und ϑ, so beschreibt (r, ϑ, ϕ) einen Breitenkreis oder Parallelkreis bei der geographischen Breite ϑ auf S_r. Man nennt ϕ auch Längengrad und ϑ Breitengrad. Wie die Bezeichnungen schon andeuten, werden Kugelkoordinaten u. a. in der Geographie zur Lagebeschreibung durch geographische Koordinaten benutzt.

Für die aufeinander senkrecht stehenden (ortsabhängigen) Einheitsvektoren „in Richtung von“ r bzw. ϑ bzw. ϕ gilt mit den kartesischen Einheitsvektoren e_x, e_y, e_z: \begin{eqnarray}\begin{array}{rrrrrrr}{e}_{r} & = & \cos \vartheta \cos \varphi\,{e}_{x} & + & \cos \vartheta \sin \varphi\,{e}_{y} & + & \sin \vartheta\,{e}_{z}\\ {e}_{\vartheta } & = & -\sin \vartheta \cos \varphi\,{e}_{x} & – & \sin \vartheta \sin \varphi\,{e}_{y} & + & \cos \vartheta\,{e}_{z}\\ {e}_{\varphi } & = & -\sin \varphi\,{e}_{x} & + & \cos \varphi\,{e}_{y} & & \end{array}\end{eqnarray}

Umgekehrt hat man: \begin{eqnarray}\begin{array}{rrrrrrr}{e}_{x} & = & \cos \vartheta \cos \varphi\,{e}_{r} & – & \sin \vartheta \cos \varphi\,{e}_{} & – & \sin \varphi\,{e}_{\varphi }\\ {e}_{y} & = & \cos \vartheta \sin \varphi\,{e}_{r} & – & \sin \vartheta \sin \varphi\,{e}_{\vartheta } & + & \cos \varphi\,{e}_{\varphi }\\ {e}_{z} & = & \sin \vartheta\,\,\,\qquad\,\text{}{e}_{r} & + & \cos \vartheta\,\qquad \text{}{e}_{\vartheta } & & \end{array}\end{eqnarray}

Kugelkoordinaten sind zweckmäßig bei der Behandlung von Problemen auf Kugeloberflächen oder solchen, die radiale oder Winkelsymmetrien besitzen, insbesondere zur Berechnung von Integralen, die solche Symmetrien aufweisen, mit Hilfe des Transformationssatzes. Für die durch \begin{eqnarray}F(r,\vartheta, \varphi )=(r\cos \vartheta \cos \varphi, r\cos \vartheta \sin \varphi, r\sin \vartheta )\end{eqnarray}

gegebene stetig differenzierbare Subsitutionsfunktion F : ℝ³ → ℝ³ gilt \begin{eqnarray}\det {F}{^{\prime} }(r,\vartheta, \varphi )=-{r}^{2}\cos \vartheta, \end{eqnarray}

und wenn K eine kompakte Jordan-meßbare Teilmenge von \(G:=(0,\infty )\times (-{\scriptstyle \frac{\pi }{2}},{\scriptstyle \frac{\pi }{2}})\times (0,2\pi )\) und f : F(K) → ℝ stetig ist, liefert der Transformations-satz mit \(\begin{eqnarray}{\mathfrak{x}}=(x,y,z)\end{eqnarray}\) und \(\begin{eqnarray}{\mathfrak{n}}=(r,\vartheta, \varphi )\end{eqnarray}\)\begin{eqnarray}\displaystyle \mathop{\int }\limits_{F(K)}f({\mathfrak{x}})d{\mathfrak{x}}=\displaystyle \mathop{\int }\limits_{K}f(F({\mathfrak{n}}))\,{r}^{2}\cos\,\vartheta\,d{\mathfrak{n}}.\end{eqnarray}

Häufig ist über einen durch Längen- und Breiten-grade begrenzten Ausschnitt einer Kugelschale zu integrieren, d. h. über einen Bereich F(K), wobei K = [r₁, r₂] × [ϑ₁, ϑ₂] × [ϕ₁, ϕ₂] ein „Quader“ in G ist. Dann hat man \begin{eqnarray}\begin{array}{l}\displaystyle \mathop{\int }\limits_{F(K)}f(x,y,z)d(x,y,z)=\\\qquad \displaystyle \underset{{\varphi }_{1}}{\overset{{\varphi }_{2}}{\int }}\displaystyle \underset{{\vartheta }_{1}}{\overset{{\vartheta }_{2}}{\int }}\displaystyle \underset{{r}_{1}}{\overset{{r}_{2}}{\int }}f(F(r,\vartheta, \varphi )){r}^{2}\cos \vartheta\,dr\,d\vartheta\,d\varphi.\end{array}\end{eqnarray}

Die Reihenfolge der Integrationen ist dabei beliebig. Die Größe \begin{eqnarray}dV={r}^{2}\cos \vartheta\,dr\,d\vartheta\,d\varphi\end{eqnarray}

läßt sich als „infinitesimales Volumenelement“ in Kugelkoordinaten deuten. Entsprechend hat man bei Oberflächenintegralen „Flächenelemente“ r dr dϑ, r² cos ϑ dϑ dϕ und r cos ϑ dϕ dr, und bei Wegintegralen das „Bogenlängenelement“ oder „Linienelement“ ds² = dr² + r²dϑ² + r² cos²ϑ dϕ².