Lexikon der Mathematik: Kurvendiskussion
Untersuchen der Eigenschaften reellwertiger, auf Teilmengen von ℝ definierter Funktionen f mit Mitteln der Analysis.
Dazu können zählen:
- Bestimmen des (maximalen) Definitionsbereichs und des Wertebereichs von f.
- Untersuchen von f auf Periodizität und Geradheit oder Ungeradheit oder sonstige Invarianzund Symmetrieeigenschaften (und damit Reduktion des zu untersuchenden Bereichs).
- Untersuchen von f auf Stetigkeit und Differenzierbarkeit und ggf. Bestimmen der Ableitungen f, f′, f″.
- Berechnen der Funktionswerte von f an ausgewählten Stellen und Erstellen einer Wertetabelle.
- Bestimmen der Nullstellen von f und der Bereiche, wo f positiv bzw. negativ ist.
- Untersuchen des Monotonieverhaltens von f. Falls f differenzierbar ist, kann hierzu die Ableitung f′ herangezogen werden.
- Bestimmen lokaler und globaler Extremwerte von f. Auch hierzu kann f′ benutzt werden, wenn f differenzierbar ist.
- • Untersuchen des Krümmungsverhaltens von f, also Untersuchen von f auf Konvexität und Konkavität und damit Bestimmen der Wendepunkte. Ist f zweimal differenzierbar, kann hierzu die zweite Ableitung f″ betrachtet werden.
- Beschreiben des Grenzverhaltens von f an bestimmten Stellen (Unstetigkeitstellen, Lücken oder Rand des Definitionsbereichs).
- Bestimmen von Asymptoten von f und der Lage des Graphen von f relativ zu diesen.
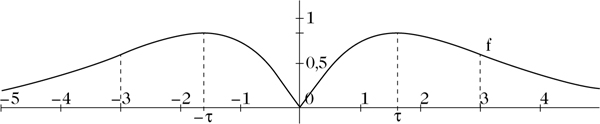
Kurvendiskussion: Die Funktion f(x) = (x2 + |x|)e−|x|
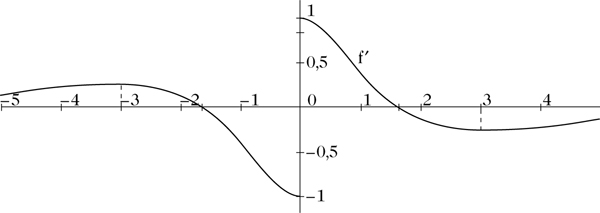
Kurvendiskussion: Die Funktion f′
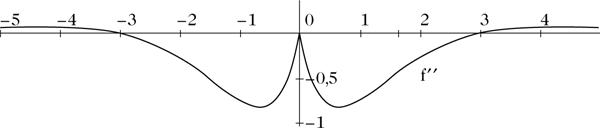
Kurvendiskussion: Die Funktion f″
Mittels der dabei über f gewonnenen Erkenntnisse kann zumeist eine Skizze des Graphen von f erstellt werden.
Ein einfaches Beispiel: Durch
wird eine Funktion f : ℝ → ℝ definiert. Da f gerade ist, genügt es, im folgenden x ≥ 0 zu betrachten: Nach den Differentiationsregeln ist f differenzierbar in (0, ∞) mit
für x > 0. Wegen
für ϵ ↓ 0 ist f an der Stelle 0 rechtsseitig differenzierbar mit \(\begin{eqnarray}{{f}{^{\prime} }}_{+}(0)=1\end{eqnarray}\). Da f gerade ist, folgt \(\begin{eqnarray}{{f}{^{\prime} }}_{-}(0)=-1\ne {{f}{^{\prime} }}_{+}(0)\end{eqnarray}\), d. h. f ist nicht differenzierbar an der Stelle 0. f′ ist als Ableitung einer geraden Funktion ungerade. Ferner ist f′ differenzierbar in (0, ∞) mit
<?PageNum _233
für x > 0. f″ ist als Ableitung einer ungeraden Funktion gerade. Es gilt f(0) = 0 und f(x) > 0 für x > 0. Folglich hat f an der Stelle 0 ein strenges globales Minimum. Da P(x)e−x → 0 (x → ∞) gilt für jedes Polynom P, hat man f(x) → 0 für x → ∞. Auflösen von f′(x) = 0 liefert \(x=\tau ={\scriptstyle \frac{1}{2}}(1+\sqrt{5})\). Wegen f″(τ ) = (1 − 2τ)e−τ< 0 hat f an der Stelle τ ein strenges lokales Maximum. Dies ist das einzige und daher das globale Maximum von f in (0, ∞). Auflösen von f″(x) = 0 im Bereich (0, ∞) liefert x = 3. Für 0 < x< 3 ist f″(x) < 0, d. h. f streng konkav, und für x > 3 ist f″(x) > 0, d. h. f streng konvex. Daher hat f an der Stelle 3 einen Wendepunkt. Da f gerade ist, ist an der Stelle 0 kein Wendepunkt.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.