Lexikon der Mathematik: L-R-Fuzzy-Zahl
eine Fuzzy-Zahl \(\tilde{M}\), deren Zugehörigkeitsfunktion sich mit geeigneten ReferenzfunktionenL und R darstellen läßt als
Der eindeutig bestimmte Wert m mit μM(m) = 1 = L(0) ist der Gipfelpunkt der Fuzzy-Zahl. Die Größen α und β werden linke bzw. rechte Spannweite von \(\tilde{M}\) genannt. Für α = β = 0 ist \(\tilde{M}\) vereinbarungsgemäß eine gewöhnliche reelle Zahl, andererseits wird \(\tilde{M}\) mit wachsenden Spannweiten α und β immer unschärfer.
Für L-R-Zahlen ist die verkürzte Notation \(\tilde{M}={(m;\alpha; \beta )}_{LR}\) üblich.
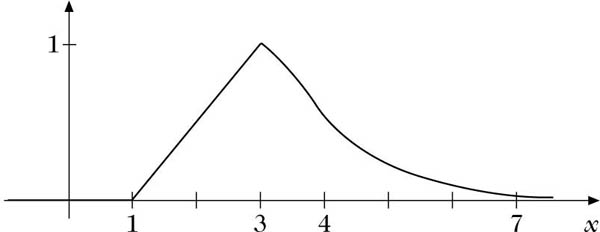
L-R-Fuzzy-Zahl \(\tilde{M}={(3;2;1)}_{LR}\) mit L(u) = max(0,1 −u) und \(R(u)=\frac{1}{1+{u}^{2}}\).
Die Bedeutung von L-R-Fuzzy-Zahlen liegt darin, daß die arithmetischen Rechenoperationen besonders einfach durchzuführen sind (Fuzzy-Arithmetik, L-R-Fuzzy-Intervall).
Bei Fuzzy-Zahlen ist die erweiterte Subtraktion i. allg. nicht die Umkehrung der erweiterten Addition. Dies läßt sich leicht für L-R-Fuzzy-Zahlen mit der gleichen Referenzfunktion L(u) = R(u) zeigen:
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.