Weglänge, das Supremum der Längen dem Weg einbeschriebener Polygon-züge.

Es sei s ein Weg, also \begin{eqnarray}s:[a,b]\to {{\mathbb{R}}}^{n}\space \text{stetig}\end{eqnarray}

für a, b ∈ ℝ mit a < b und n ∈ ℕ. Zu einer Zerlegung \begin{eqnarray}\mathfrak{Z}:\quad\text{}a={t}_{0}\lt {t}_{1}\lt \cdots {t}_{k}=b\end{eqnarray}

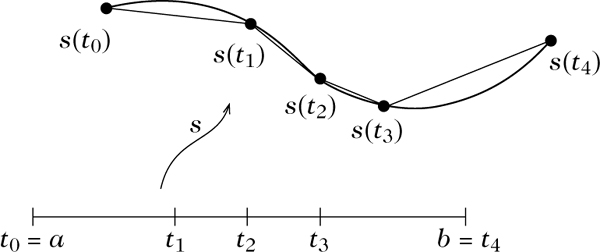
(k ∈ ℕ) von [a, b] betrachtet man die Länge des zugehörigen einbeschriebenen Polygonzugs durch die Punkte s(t₀), s(t₁),…s(t_k), also die Größe \begin{eqnarray}\ell (\mathfrak Z,s):=\displaystyle \sum _{k=1}^{k}\|s({t}_{\kappa })-s({t}_{k-1})\|\end{eqnarray}

mit einer vorgegebenen Norm ∥ ∥ auf dem ℝⁿ, wobei man meist von der euklidischen Norm ∥ ∥ = ∥ ∥₂ ausgeht.

Das Supremum ℓ(s) (in [0, ∞]) der ℓ(Ʒ, s) über alle Zerlegungen Ʒ von [a, b] heißt dann Länge des Weges s. Ist diese endlich, so heißt s rektifizierbar. (Nach der Dreiecksungleichung wird ℓ(Ʒ, s) bei Hinzunahme von Punkten (,Verfeinerung‘) höchstens größer. Man kann so das Supremum auch als allgemeinen Grenzwert auffassen.)

Natürlich können als Zielbereiche statt ℝⁿ auch beliebige Banachräume zugelassen werden.

Mit den Koordinatenfunktionen s_ν (ν = 1,…,n) von s gilt:

s ist genau dann rektifizierbar, wenn alle Koordinatenfunktionen s_ν von beschränkter Variation sind.

Ist s stetig differenzierbar, so hat man \begin{eqnarray}\ell (s)=\displaystyle \underset{a}{\overset{b}{\int }}\|{s}^{^{\prime} }(t)\|dt.\end{eqnarray}

Ein solcher Weg ist also stets rektifizierbar, und seine Weglänge kann bequem über die angegebene Formel berechnet werden. Dies gilt dann entsprechend noch für stückweise stetig differenzierbare Wege.

Als Beispiel sei auf diese Weise im ℝ² der Umfang des Kreises um (0, 0) mit Radius r > 0 berechnet: Hier ist s(t) := (r cos t, r sin t) (t ∈ [0, 2π]), also s′(t) = (− r sin t, r cos t). Somit ist ∥s′(t)∥₂ = r, und schließlich ℓ(s) = 2πr.

Gelegentlich spricht man auch für f : [a, b] → ℝ vom „Weg“ f und meint dann den durch \begin{eqnarray}s(t):=\left(\begin{array}{c}t\\ f(t)\end{array}\right)\end{eqnarray}

<?PageNum_251 definierten Weg s. Dieser Weg ist genau dann rektifizierbar, wenn f von beschränkter Variation ist. Für stetig differenzierbares f gilt offenbar \begin{eqnarray}\ell \left( s \right) = \int\limits_a^b {\sqrt {1 + \left( {f\prime \left( t \right)} \right)^2 } dt.}\end{eqnarray}