Lexikon der Mathematik: Lagrange-Interpolation
klassische Interpolationsmethode, bei der eine stetige Funktion durch eine endliche Menge von Werten eindeutig festgelegt wird.
Lagrange-Interpolation wird in der Numerischen Mathematik und der Approximationstheorie behandelt.
Es sei G ={g0, g1, …, gN} ein System von N + 1 linear unabhängigen, stetigen, reell- oder komplexwertigen Funktionen, definiert auf einem Intervall [a, b], einem Gebiet G ⊂ ℂ, oder einem Kreis T. Weiter sei X ={x0, …, xN} eine Menge von N + 1 Punkten aus [a, b], bzw. T, mit der Eigenschaft x0<… < xN. Das Problem der Lagrange-Interpolation hinsichtlich G und X besteht nun darin, für reelle Werte ci, i = 0, …, N, eine eindeutige Funktion
mit der Eigenschaft
zu finden. Falls für beliebige ci stets eine solche Funktion g existiert, so ist das Problem der Lagrange-Interpolation hinsichtlich G und X lösbar. X heißt in diesem Fall Lagrange-Interpolationsmenge für G.
Verallgemeinerungen der Lagrange-Interpolation, bei denen neben den Funktionswerten von g auch gewisse Ableitungen vorgeschrieben werden, nennt man Hermite-Interpolation bzw. Birk-hoff-Interpolation.
Bei der Lagrange-Interpolation spielen strukturelle Eigenschaften des zugrundeliegenden Systems G ein Rolle. Es ist bekannt, daß das Problem der Lagrange-Interpolation genau dann für jede beliebige Wahl von X lösbar ist, wenn G ein Tschebyschew-System bildet. Ein solches System G bilden beispielsweise die Polynome vom Grad N,
In diesem Fall läßt sich für jedes vorgegebene X und beliebig vorgegebene Werte ci das Interpolationspolynom g in der Lagrange-Darstellung
angeben. Hierbei sind die Lagrange-Polynome (auch Lagrange-Fundamentalpolynome oder Lagrangesche Grundpolynome genannt) lN,i definiert durch
Es gilt offenbar
Die Lagrange-Polynome sind daher linear unabhängig. Sie hängen nur von den xi, nicht von den ci ab.
Man faßt diese Tatsache im klassischen Interpolationssatz von Lagrange zusammen:
Es seien N + 1 ∈ ℕ verschiedene Punkte x0,…,xN aus ℝ oder ℂ und N + 1 beliebige Zahlen c0,…,cN gegeben. Dann existiert genau ein Polynom p vom Grad höchstens N derart, daß p(xi) = ci für i = 1,…,N. Dieses Polynom besitzt die Darstellung
mit den durch (1) definierten Lagrange-Polynomen lN,i.
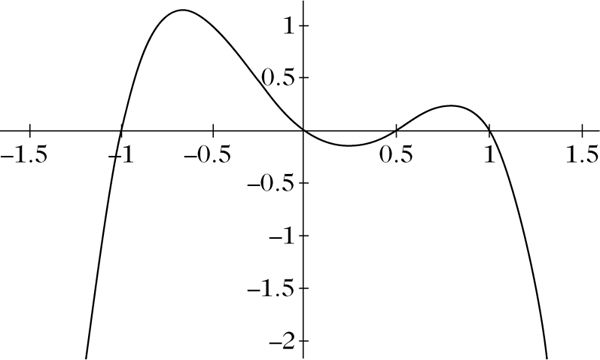
Das Polynom l4,1 für x0 = −1, x1 = −0.5, x2 = 0, x3 = 0.5, x4 = 1.
Ein Maß für die Güte des Approximationsverhaltens des Interpolationspolynoms auf einem Intervall [a, b] ist die Lebesgue-Konstante
Wählt man beispielsweise äquidistante Punkte, d. h. xi+1 − xi = const, so ist die Lebesgue-Konstante recht groß, was sich im allgemeinen negativ auswirkt. Andererseits ist bekannt, daß eine gute Wahl der Menge X durch die sogenannten Tschebyschew-Punkte
gegeben ist. Dies sind die Nullstellen des Tschebyschew-Polynoms. Für sie ist die Lebesgue-Konstante vergleichsweise klein.
Numerisch deutlich stabiler als die Lagrange-Darstellung ist die Newtonsche Interpolationsformel für g.
Falls G kein Tschebyschew-System bildet, so ist das Problem der Lagrange-Interpolation hinsichtlich G und X nur unter gewissen Zusatzvoraussetzungen an X lösbar. Betrachtet man beispielsweise ein System G von Splinefunktionen
wobei a ≤ t0< t1<… < tk−1 ≤ b und (z)+ = max{0, z}, so gilt der folgende Satz von Schoenberg und Whitney aus dem Jahr 1953.
Das Problem der Lagrange-Interpolation hinsichtlich G und X ={x0<… < xN+k} ist genau dann lösbar, wenn X wie folgt über [a, b] verteilt ist:
Einfache Charakterisierungen von Lagrange-Interpolationsmengen X dieser Art sind nicht für jedes System G möglich. So weiß man beispielsweise, daß für Splines definiert auf einem Kreis T, sogenannte periodische Splines, eine solche Verteilungsbedingung im allgemeinen nur notwendig, jedoch nicht hinreichend ist.
Für Systeme G von multivariaten Funktionen führt das Problem der Lagrange-Interpolation auf moderne und komplexe mathematische Fragestellungen, die derzeit von Approximationstheoretikern untersucht werden. Hierbei sind vor allem Systeme G multivariater Polynome und multivariater Splines von großer Bedeutung.
[1] Hämmerlin, G.; Hoffmann, K.-H.: Numerische Mathematik. Springer-Verlag Berlin, 1989.
[2] Schönhage, A.: Approximationstheorie. de Gruyter & Co. Berlin, 1971.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.