Filter, der als Faltung f ∗ h einer Maske h mit dem Signal f dargestellt werden kann.

Mit Hilfe des Faltungssatzes ist ihre Wirkung im Frequenzbereich durch

\begin{eqnarray}\widehat{f*h}=\hat{f}* \hat{h}\end{eqnarray}

beschrieben.

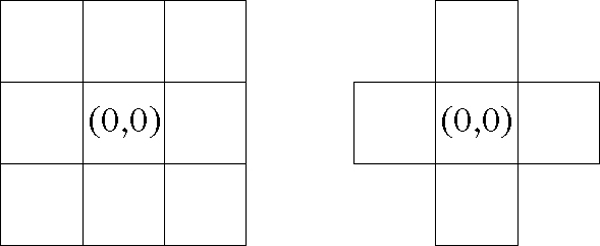
Beispiele für lineare Faltungsfilter sind Tiefpaßoder Hochpaßfilter. Im eindimensionalen Fall ist ein Filter durch eine Anzahl von Koeffizienten (Maske) beschrieben, im zweidimensionalen Fall wird die Maske als rechteckiges Schema dargestellt.

In der Praxis gängige Filter, z. B. zur Entrauschung oder der Konturverbesserung von Bildern, sind von der Größe 3 × 3 oder 5 × 5.