logisches Netzwerk, informationstheoretische Realisierung eines Schaltkreises.

Man unterscheidet zwischen kombinatorischen und sequentiellen Schaltkreisen. Ein kombinatorischer Schaltkreis mit n Eingängen und m Ausgängen über einer Bausteinbibliothek Ω, die nur Boolesche Funktionen mit jeweils einem Booleschen Ausgang enthält, ist durch ein Tupel S = (G, typ, pe, pa) definiert, wobei gilt:

1. G = (V, E) ist ein azyklischer gerichteter Graph, bei dem es für jeden Knoten v ∈ V eine Numerierung der einlaufenden Kanten gibt. Diese Knotenorientierung von G ist gegeben durch eine partiell spezifizierte injektive Abbildung I : V × ℕ → E. Ist i größer oder gleich 1 und kleiner oder gleich dem Eingangsgrad eines Knoten v ∈ V, dann ist I(v, i) definiert und gibt die i-te Kante an, die in v einläuft.
2. typ : V → Ω ∪ {in, out} ist eine Abbildung, die jedem Knoten v ∈ V entweder eine Funktion der Bausteinbibliothek Ω, die Bezeichnung in, oder die Bezeichnung out zuordnet. Hierbei müssen genau n Knoten den Typ in und genau m Knoten den Typ out zugeordnet bekommen. Der Eingangsgrad eines Knotens v ∈ V mit typ(v) = in muß 0 sein. Der Ausgangsgrad eines Knotens v ∈ V mit typ(v) = out muß ebenfalls 0 sein; der Eingangsgrad eines solchen Knotens muß 1 sein. Ist typ(v) aus Ω, so muß der Eingangsgrad von v der Stelligkeit von typ(v) entsprechen.
3. pe : {1,…,n} → {v ∈ V : typ(v) = in} bzw. pa : {1,…, m} → {v ∈ V : typ(v) = out} sind bijektive Abbildungen. Sie geben die Numerierung der mit in bzw. mit out markierten Knoten aus V an. pe(i) heißt i-ter primärer Eingang, pa(i) heißt i-ter primärer Ausgang.

Die durch den kombinatorischen Schaltkreis S berechnete Funktion f_S : {0,1}ⁿ → {0, 1} ist definiert durch \begin{eqnarray}{f}_{S}(\alpha )=({f}_{{y}_{1}}(\alpha ),\ldots, {f}_{{y}_{m}}(\alpha )),\end{eqnarray} wobei \begin{eqnarray}{y}_{i}=I(pa(i),\,\,1)\,\,\,\,\,\forall i\in \{1,\ldots, m\}\end{eqnarray} ist. Die Boolesche Funktion \({f}_{{y}_{i}}\) ist eindeutig bestimmt durch:

1. Ist v ∈ V, typ(v) = in und pe(i) = v, dann ist die durch den primären Eingang v berechnete Boolesche Funktion f_v : {0, 1}ⁿ → {0, 1} definiert durch \begin{eqnarray}{f}_{v}({\alpha }_{1},\ldots, {\alpha }_{n})={\alpha }_{i}\end{eqnarray} für alle (α₁,…, α_n) ∈ {0,1}ⁿ. Ist e eine beliebige Kante, die aus dem Knoten v herausläuft, so setzen wir die durch e berechnete Boolesche Funktion f_e gleich f_v.
2. Ist v ∈ V, typ(v) = g ∈ Ω mitg : {0, 1}^q → {0, 1} und für 1 ≤ k ≤ q die Kante e_k der k-te Eingang von v, d.h. I(v, k) = e_k, dann ist die durch v berechnete Boolesche Funktion f_v : {0, 1}ⁿ → {0, 1} definiert durch \begin{eqnarray}{f}_{v}(\alpha )=g({f}_{{e}_{1}}(\alpha ),\ldots, {f}_{eq}(\alpha ))\end{eqnarray} für α ∈ {0, 1}ⁿ. Wieder wird die durch eine aus v herauslaufende Kante e berechnete Boolesche Funktion f_e gleich f_v gesetzt.

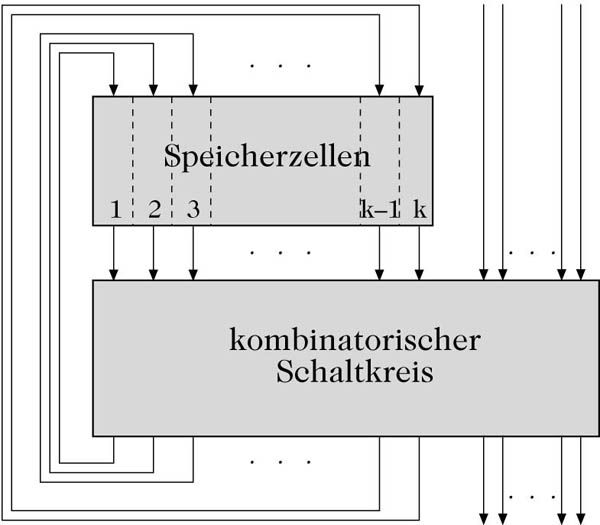
Ein sequentieller Schaltkreis realisiert einen endlichen Automaten und besteht aus einem kombinatorischen Schaltkreis mit n Eingängen, m Ausgängen und k Speicherzellen, wobei k ≤ min {n, m} ist. k der n Eingänge des kombinatorischen Schaltkreises sind mit den Ausgängen der Speicherzellen und k der m Ausgänge des kombinatorischen Schaltkreises mit den Dateneingängen der Speicherzellen verbunden. In den Speicherzellen wird der jeweils aktuelle Zustand des Schaltkreises gespeichert. Die nicht mit den Speicherzellen verbundenen Eingänge des kombinatorischen Schaltkreises heißen primäre Eingänge des sequentiellen Schaltkreises; über sie werden die Eingabesymbole (endlicher Automat) eingegeben. Die nicht mit den Speicherzellen verbundenen Ausgänge des kombinatorischen Schaltkreises heißen primäre Ausgänge des sequentiellen Schaltkreises; über sie werden die Ausgabesymbole ausgegeben.

Die Kosten eines logischen Schaltkreises sind gegeben durch die Anzahl der Knoten im Graphen G, falls es sich um einen kombinatorischen Schaltkreis handelt. Bei sequentiellen Schaltkreisen kommen zu den Kosten des kombinatorischen Teils noch zusätzliche Kosten hinzu, die proportional zu der Anzahl der in dem Schaltkreis verwendeten Speicherzellen sind.

Von großer Bedeutung waren in der Vergangenheit und sind auch heute noch zweistufige kombinatorische Schaltkreise, sog. PLAs oder programmierbare logische Felder. In der Regel wertet ein zweistufiger kombinatorischer Schaltkreis in einer ersten Stufe parallel verschiedene Boolesche Monome aus; in der zweiten Stufe werden diese Werte über ein logisches ODER (OR-Funktion) zusammengefaßt.

Zweistufige kombinatorische Schaltkreise realisieren somit Boolesche Polynome und sind die Zieltechnologie der zweistufigen Logiksynthese. Logische Schaltkreise, die in diesem Sinne aus mehr als zwei Stufen aufgebaut sind, werden mehrstufige kombinatorische Schaltkreise genannt.