Lexikon der Mathematik: logistische Verteilung
das zu den Parametern μ, σ ∈ ℝ, σ > 0 durch die Wahrscheinlichkeitsdichte
Es wird genauer als logistische Verteilung mit den Parametern μ und σ bezeichnet. Die zugehörige Verteilungsfunktion ist durch
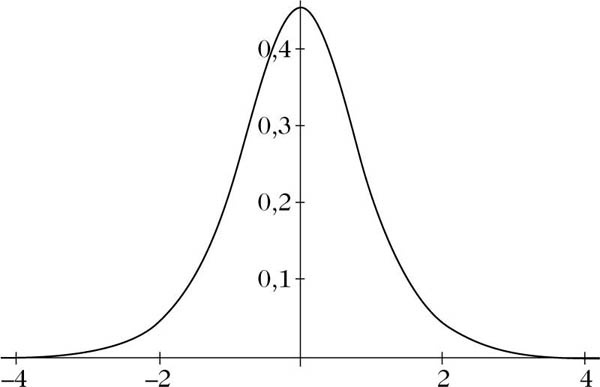
Dichte der logistischen Verteilung mit den Parametern μ = 0 und σ = 1
gegeben. Für den Erwartungswert einer Zufallsvariablen X, die eine logistische Verteilung mit den Parametern μ und σ besitzt, gilt E(X) = μ, und für die Varianz Var(X) = σ2.
Die logistische Verteilung wird häufig zur Modellierung von Wachstumsvorgängen mit Sättigung verwendet.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.