Lexikon der Mathematik: Minimalfläche
eine Fläche ℳ ⊂ ℝ3, deren mittlere Krümmungh gleich Null ist.
Minimalflächen sind Lösungen des Plateauschen Problems im Kleinen. Das bedeutet, daß für jede geschlossene, in einer genügend kleinen Kugel liegende Flächenkurve 𝒦 ⊂ ℳ, die aus ℳ ein zur Kreisscheibe homöomorphes Flächenstück ℳ0 ⊂ ℳ ausschneidet (d. h. 𝒦 ist die Randkurve von ℳ0), die Fläche ℳ0 unter allen anderen Flächen, die 𝒦 gleichfalls als Randkurve besitzen, den kleinsten Flächeninhalt hat.
Die Bestimmung aller Minimalflächen des ℝ3 ist zunächst das Problem, alle Lösungen der partiellen Differentialgleichung zweiter Ordnung für die Komponenten einer Parameterdarstellung Φ(u, v) zu bestimmen, die sich aus dem Nullsetzen von h ergibt. Schränkt man sich jedoch auf konforme Parameterdarstellungen ein, so wird diese Differentialgleichung zur Laplacegleichung und man erhält:
Jede Minimalfläche ℳ ⊂ ℝ3in konformer Parametrisierung Φ(u, v) =Re(Z(u + iv) läßt sich als Realteil einer komplexen isotropen Kurve Z(z) in ℂ3darstellen, d. h. es gilt Φ(u, v) = Re(Z(u + iv) für alle z = u + iv ∈ ℂ.
Dabei versteht man unter einer komplexen Kurve das komplexe Analogon einer parametrisierten Kurve im ℝ3, d. h., eine holomorphe Abbildung Z : 𝒰 → ℂ3 einer offenen Teilmenge 𝒰 ⊂ ℂ. Z heißt isotrop oder minimal, wenn der komplexe Tangentialvektor Z′(z) = dZ(z)/dz für alle z ∈ U die komplexe Länge Null hat, d. h., wenn \({{Z}^{^{\prime} }}_{1}^{2}(z)+{{Z}^{^{\prime} }}_{2}^{2}(z)+{{Z}^{^{\prime} }}_{3}^{2}(z)=0\) für die Ableitungen der drei Komponenten Z1, Z2, Z3 von Z gilt. Im Gegensatz zum Körper ℝ der reellen Zahlen hat in ℂ die Gleichung \({z}_{1}^{2}+{z}_{2}^{2}+{z}_{3}^{2}=0\) eine zweiparametrige Schar von Lösungen, die man z. B. durch z1 = s (1 − t2), z2 = is (1 + t2) und z3 = 2 st mit den beiden Parametern s, t ∈ ℂ beschreiben kann. Sind f(z) und g(z) zwei beliebige meromorphe Funktionen, und setzt man s = f(z) und t = g(z), so erhält man eine isotrope Kurve Z(z) = (Z1(z), Z2(z), Z3(z)) indem man
setzt und integriert. Diese Abbildung (f(z), g(z)) → Z(z), die jedem Paar meromorpher Funktionen eine minimale Kurve zuordnet, heißt Weierstraßsche Darstellungsformel.
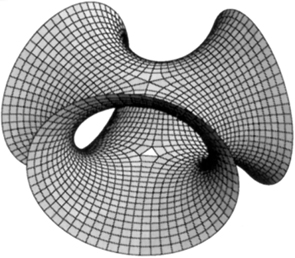
Das Trinoid ist die mathematische Beschreibung einer Seifenlamelle, die sich an drei Kreisen ausbildet.
Die einfachsten Minimalflächen sind die Ebene, das Katenoid und die Wendelfläche. Als Beispiel einer komplizierteren Minimalfläche, die Ähnlichkeit mit drei im Winkel von je 120◦ regelmäßig angeordneten halben Katenoiden hat, zeigt die Abbildung eine Darstellung des Trinoids, dessen zugehörige isotrope Kurve durch
mit t = t(z) = tanh2/3 ((3 + 3 i) z/4) gegeben ist.
Die Definition der Minimalfläche wird zum Begriff der k-dimensionalen minimalen Untermannigfaltigkeit \({\tilde{N}}^{k}\subset {M}^{n}\) einer beliebigen Riemannschen MannigfaltigkeitMn verallgemeinert, indem man an die Stelle des Flächeninhalts das k-dimensionale Volumen der Riemannschen Untermannigfaltigkeit \({\tilde{N}}^{k}\) und an die Stelle der mittleren Krümmung eine andere Invariante, den Vektor der mittleren Krümmung von \({\tilde{N}}^{k}\), setzt.
[1] Jost, J.: Differentialgeometrie und Minimalflächen. Springer Verlag, Berlin-Heidelberg-New York, 1994.
[2] Nitsche, J. C. C.: Vorlesungen über Minimalflächen. Grundlehren der mathematischen Wissenschaften 199, Springer Verlag, Berlin-New York, 1975.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.