Monte-Carlo-Simulation, Verfahren zur numerischen Lösung verschiedener mathematischer Probleme nichtstochastischen Charakters unter Benuzung von Zufallszahlen bzw. Pseudozufallszahlen, allgemeiner auch Bezeichnung für eine Simulation, d. h. rechnerischexperimentelles Nachspielen realer zufallsbehafteter Vorgänge.

Die Monte-Carlo-Methode im erstgenannten Sinne wird u. a. zur näherungsweisen Berechnung von Integralen, Lösung partieller und gewöhnlicher Differentialgleichungen sowie algebraischer Gleichungssysteme, zum Finden lokaler Extremwerte einer Funktion und zur Invertierung von Matrizen angewendet. Besonders vorteilhaft gegenüber klassischen Verfahren der praktischen Mathematik ist der Einsatz der Monte-Carlo-Methode, wenn es sich um hochdimensionale Probleme handelt. Das Prinzip der Methode ist begründet durch die Gesetze der großen Zahlen. Darüber hinaus erlaubt der aus der Statistik bekannte Zentrale Grenzwertsatz zu vorgegebener geforderter Genauigkeit der Lösung und zu vorgegebener statistischer Sicherheit die notwendige Anzahl zufälliger Experimente zu bestimmen. Zur Erläuterung betrachten wir das folgende einfache Beispiel: Es soll das Integral \begin{eqnarray}F\,=\,\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx\end{eqnarray}

einer auf [a, b] beschränkten und positiven Funktion berechnet werden. Die Monte-Carlo-Methode kann man hier auf verschiedene Weisen anwenden.

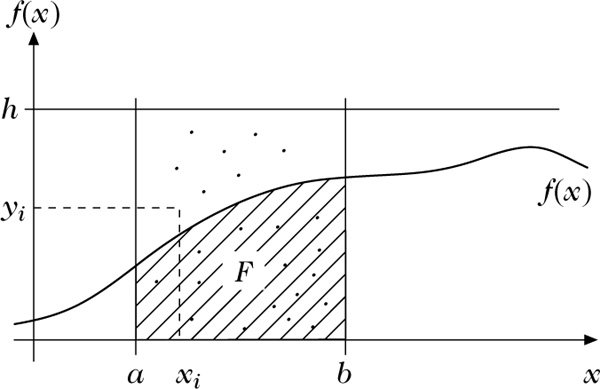
a) Ein brauchbares stochastisches Modell besteht z. B. in der Interpretation der Zahl F als geometrische Wahrscheinlichkeit (F = P(A)) des Ereignisses A, daß ein zufällig auf das Rechteck [a, b] × [0, h] geworfener Punkt unterhalb des Graphen von f, also in der in der Abbildung markierten Fläche, zu liegen kommt.

Man erzeugt nun mit Hilfe von Pseudozufallszahlengeneratoren n Paare (x_i, y_i), i = 1,…, n, von Punkten, wobei x_i gleichmäßig auf [a, b] und y_i gleichmäßig auf [0, h] verteilte Zufallszahlen sind. Die auf der Basis dieser Punkte festgestellte relative Häufigkeit h_n(A) des Ereignisses A (A ist eingetreten, falls y_i ≤ f (x_i)) liefert eine brauchbare Schätzung für F.

b) Bei einer zweiten Methode interpretiert man F als den mit (b − a) multiplizierten Erwartungswert F = (b − a)Ef(X) einer Zufallsgröße X, die gleichmäßig auf [a, b] verteilt ist. Eine Schätzung für F erhält man dann durch \(\hat{F}\,=\,(b\,-\,a)\bar{f}\), wobei \(\bar{f}\) das arithmetische Mittel von f \begin{eqnarray}\bar{f}\,=\,\frac{\displaystyle {\sum }_{i=1}^{n}f({x}_{i})}{n}\end{eqnarray}

auf der Basis von n gleichmäßig auf [a, b] verteilten Zufallszahlen x_i ist.

Es läßt sich zeigen, daß die zweite Methode Schätzfunktionen mit geringerer Varianz liefert. Eine weitere Varianzreduktion erhält man, indem man im zweiten Modell andere Verteilungen für X verwendet, wobei deren optimale Wahl allerdings von f abhängt.

Ein historisch erstes Beispiel für die Anwendung der Monte-Carlo-Methode ist die näherungsweise Ermittlung der Zahl π mit Hilfe des Buffonschen Nadelproblems.

Unter der Monte-Carlo-Simulation versteht man auch das rechnerisch-experimentelle Nachspielen realer zufallsbehafteter Vorgänge. Solche Vorgänge werden in der Mathematik durch stochastische Modelle beschrieben. Die Monte-Carlo-Simulation wird dann verwendet, wenn theoretische Berechnungen sehr aufwendig sind, z. B. bei Untersuchungen in der Warteschlangentheorie. Bei der Monte-Carlo-Simulation werden Realisierungen aller im Modell eingeschlossenen Zufallsgrößen durch Pseudozufallszahlengeneratoren erzeugt und die entsprechenden gesuchten Leistungskenngrößen geschätzt. Zur Durchführung von Simulationen insbesondere von Bedienungssystemen auf dem Computer wurde eine Vielzahl von Simulationssprachen geschaffen, wie z. B. GPSS oder AWSIM. Diese enthalten spezifische Sprachbestandteile zur Beschreibung der Elemente des zu simulierenden Systems, zu deren Generierung und Auslöschung, zur Erzeugung von Zufallszahlen, zur Zeitablaufsteuerung, zur statistischen Parameterschätzung, zur Animation der Abläufe u. a.m., wodurch die Programmierung einer Simulation komplexer Systeme erleichtert wird.

Der Name der Methode geht auf die in Monte-Carlo durchgeführten Glücksspiele zurück und wurde 1949 von N. Metropolis und S. Ulam erstmals verwendet. Die Monte-Carlo-Methode kam aber erst durch die Entwicklung der modernen Computertechnik im 20. Jahrhundert zu ihrer eigentlichen Entfaltung.

[1] Hengartner, W.; Theodorescu, R.: Einführung in die Monte-Carlo-Methode. Deutscher Verlag der Wissenschaften, Berlin, 1978.
[2] Kramer, U.; Neculau, M.: Simulationstechnik. Carl Hanser Verlag München Wien, 1998.
[3] Rubinstein, R.Y.: Simulation and the Monte-Carlo method. Wiley, New York, 1981.