Hilfsmittel zur Darstellung funktionaler Beziehungen zwischen drei Variablen.

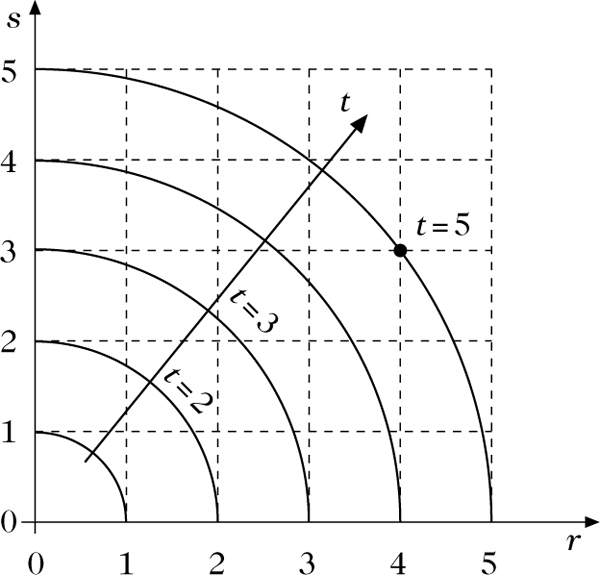
Die Grundform der Netztafel besteht aus drei bezifferten Kurvenscharen, je einer für jeden der drei Scharparameter r, s, t. Sie verlaufen in einem ebenen kartesischen Koordinatensystem. Die einem Wertetripel (r, s, t) entsprechenden Kurven der Scharen, die der Beziehung F(r, s, t) = 0 genügen, schneiden sich in einem Punkt (vgl. Abbildung). Ein Ablesebeispiel: Sei \(t=f(r,s)=\sqrt{{r}^{2}+{s}^{2}}\).

Für r = 4, s = 3 liest man ab:

\begin{eqnarray}t=\sqrt{{4}^{2}+{3}^{2}}=5.\end{eqnarray}

Wenn zwei Kurvenscharen achsenparallel zu den Koordinatenachsen x und y verlaufen und die dritte der Bedingung F(x, y, t) = 0 genügt, heißt die Netztafel auch Schichtlinientafel. Sind alle drei Kurvenscharen allgemeine Geraden, heißt sie auch Geradentafel. Zu jeder Netztafel-Form gehören entsprechende Schlüsselgleichungen.