die 1665 von Isaac Newton gefundene Reihendarstellung von π.

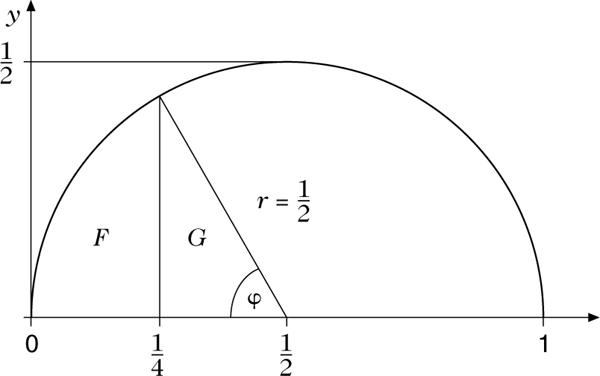
Newton betrachtete den Halbkreis mit Radius \(r=\displaystyle\frac{1}{2}\) und Mittelpunkt \(\left(\displaystyle\frac{1}{2},0\right)\), also \(y=\sqrt{x-{x}^{2}}\) (vgl. Abb.).

Durch binomisches Entwickeln von \(\sqrt{1-x}\) erhielt er die Segmentfläche F: \begin{eqnarray}\begin{array}{lll}F & = & \displaystyle \underset{0}{\overset{\frac{1}{4}}{\int }}\sqrt{x-{x}^{2}}dx=\displaystyle \underset{0}{\overset{\frac{1}{4}}{\int }}\sqrt{x}\sqrt{1-x}\,dx\\ & = & \displaystyle \underset{0}{\overset{\frac{1}{4}}{\int }}{x}^{\frac{1}{2}}\displaystyle \sum _{n=0}^{\infty }\left(\begin{array}{c}\frac{1}{2}\\ n\end{array}\right){(-x)}^{n}dx\\ & = & \displaystyle \sum _{n=0}^{\infty }{(-1)}^{n}\left(\begin{array}{c}\frac{1}{2}\\ n\end{array}\right)\displaystyle\frac{1}{(2n+3){2}^{2n+2}}.\end{array}\end{eqnarray} Der Satz des Pythagoras liefert \(h=\sqrt{3/4}\), also \begin{eqnarray}G=\displaystyle\frac{1}{2}\cdot \displaystyle\frac{1}{4}h=\sqrt{3}/32.\end{eqnarray}Weiter gilt \(\varphi =\arccos \displaystyle\frac{1}{2}=\displaystyle\frac{\pi }{3}\) und daher \begin{eqnarray}F+G=\displaystyle\frac{\varphi }{2\pi }\cdot \pi {r}^{2}=\displaystyle\frac{\pi }{24}.\end{eqnarray}Mit der sich ergebenden Formel \begin{eqnarray}\begin{array}{lll}\pi & = & 24(F+G)\\ & = & \displaystyle\frac{3}{4}\sqrt{3}+6\displaystyle \sum _{n=0}^{\infty }{(-1)}^{n}\left(\begin{array}{c}\frac{1}{2}\\ n\end{array}\right)\displaystyle\frac{1}{(2n+3){4}^{n}}\\ & = & \displaystyle\frac{3}{4}\sqrt{3}+6\left(\displaystyle\frac{1}{3}-\displaystyle\frac{1}{2}\cdot \displaystyle\frac{1}{5\cdot 4}-\displaystyle\frac{1}{8}\cdot \displaystyle\frac{1}{7\cdot {4}^{2}}-\cdots \right)\end{array}\end{eqnarray} berechnete Newton 15 Dezimalstellen von π.