Lexikon der Mathematik: Newtonverfahren
eine der wichtigsten Methoden zur numerischen Approximation von Nullstellen einer Funktion und – damit verbunden – zur Approximation lokaler Extremalpunkte von Optimierungsproblemen.
Die Einsatzbereiche des Newtonverfahrens sind so vielfältig, daß hier nur ein kleiner Eindruck vermittelt werden kann. Die Methode ist sowohl theoretisch als auch praktisch von unschätzbarer Bedeutung.
Die elementarste Form der Newtonmethode ist ihre Anwendung auf die Bestimmung einer Nullstelle einer stetig differenzierbaren Funktion f : [a, b] → ℝ. Das Verfahren versucht, iterativ von einem Startpunkt x0 ∈ (a, b) aus eine Folge {xk, k ∈ ℕ} zu konstruieren, die gegen eine Nullstelle von f in (a, b) konvergiert. Dabei berechnet sich die neue Iterierte xk+1 aus der alten xk gemäß
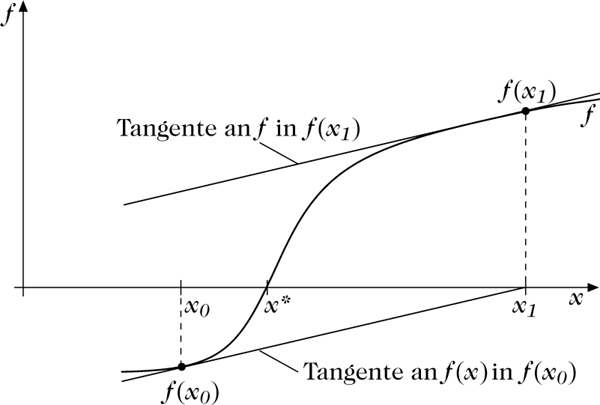
Newtonverfahren: Die Tangentengleichung an f(x) in f(xk) ist f′(xk) · x + f(xk) − f′(xk) · xk; Schnittpunkt mit der x-Achse ist xk+1 = xk − f′(xk)−1 · f(xk). Die Abbildung zeigt zwei Newtonschritte von x0 aus.
Wie man unschwer sieht, läßt sich das Newtonverfahren ebenfalls als Eulersches Polygonzugverfahren zur näherungsweisen Lösung der Differentialgleichung
Schon im obigen eindimensionalen Fall zeigen sich zentrale Fragestellungen in Zusammenhang mit dem Newtonverfahren, wie etwa: Für welche Startwerte x0 konvergiert die Methode gegen eine Nullstelle von f; gegen welche Nullstelle konvergiert das Verfahren (falls überhaupt), wenn mehrere Nullstellen vorhanden sind; wie schnell konvergiert das Newtonverfahren? Die nächste Abbildung zeigt ein einfaches Beispiel, in dem keine Konvergenz vorliegt.
Am Beispiel sieht man, daß die Tangente an f dort, wo die Ableitung fast verschwindet, eine weit von der Nullstelle entfernte nächste Newtoniterierte liefert. Die geometrische Idee hinter diesem Beispiel führt zu folgendem recht einfach beweisbaren Konvergenzkriterium.
Divergenz des Newtonverfahrens
Sei f : [a, b] → ℝ eine dreimal stetig differenzierbare Funktion, die in \(\bar{x}\in (a,b)\)eine Nullstelle habe. Gelte ferner f′(x) = 0 in einer Umgebung U von \(\bar{x}\)(d. h. insbesondere, daß \(\bar{x}\)eine einfache Nullstelle ist). Dann konvergiert das Newtonverfahren für f für jeden Startpunkt x0 ∈ U gegen die Nullstelle \(\bar{x}\). Die Konvergenzgeschwindigkeit ist quadratisch, d. h., es gibt eine Konstante C > 0, so daß
Letzteres bedeutet, daß sich die Anzahl der korrekten Stellen mit jedem Iterationsschritt nahezu verdoppelt (in Abwesenheit von Rundungsfehlern). Genauer kann man sogar zeigen, daß
Während obiges Kriterium Ableitungen bis zur dritten Ordnung verwendet und diese über einer offenen Menge U Einschränkungen unterwirft, gibt es andere Kriterien, die höhere Differenzierbarkeitsordnungen von f verlangen, dafür aber nur Bedingungen an die Ableitungen in der aktuellen Newtoniterierten stellen. Ein solches Kriterium stellt etwa die α-Theorie von Smale bereit.
I. allg. ist die Frage nach Konvergenzbereichen von immenser Schwierigkeit und Gegenstand intensiver Forschung. Die Frage nach den sogenannten Einzugsbereichen verschiedener Nullstellen (d. h. den Mengen von Startwerten, für die das Newtonverfahren gegen die entsprechende Nullstelle konvergiert) beispielsweise führt in die Theorie der dynamischen Systeme.
Ein noch recht einfaches Kriterium für einen Spezialfall liefert folgender Satz:
Es sei f ein Polynom r-ten Grades, r > 1, d. h.
Dann liefert das Newtonverfahren für jeden Startwertx0 >ξ1eine gegen ξ1konvergente monoton fallende Folge. Diese Konvergenz ist im Fall r ≥ 2 streng monoton.
Durch Abdivision lassen sich in dem durch den Satz beschriebenen Fall sukzessive sämtliche Nullstellen von f iterativ bestimmen.
Ersetzt man den in obiger Formel auftretenden Differentialquotienten f′(xk) durch den Differenzenquotienten
Eine geradlinige Verallgemeinerung des bisher gesagten ist für mehrdimensionale Abbildungen möglich. Ist f : ℝn → ℝn differenzierbar, so definiert man die Newtonabbildung Nf : ℝn → ℝn zu f durch
Es ist unmittelbar einsichtig, daß das Newtonverfahren auch eine wesentliche Rolle bei der Suche nach Extremalpunkten spielt; die Mehrzahl der bekannten notwendigen und hinreichenden Optimalitätskriterien differenzierbarer Probleme lassen sich in Form von Gleichungssystemen und damit letztlich als Nullstellenprobleme beschreiben. Zahlreiche Verfahren benutzen dabei Varianten der Methode von Newton, so z. B. das DFP-Verfahren, das BFGS-Verfahren, viele innere-Punkte-Methoden, das Lagrange-Newton-Verfahren, Homotopieverfahren etc.
Eine Verallgemeinerung für die Situation, wenn die Matrix Df(x) nicht invertierbar ist, liefern Verfahren, die dem obigen Zugang ähneln, aber statt Inversen Pseudo-Inverse verwenden.
[1] Hämmerlin, G.; Hoffmann K.-H.: Numerische Mathematik. Springer-Verlag Heidelberg/Berlin, 1991.
[2] Meinardus, G.; Merz G.: Praktische Mathematik I, II. BI-Wissenschaftsverlag Mannheim, 1979/1982.
[3] Stoer, J.: Einführung in die Numerische Mathematik I. Springer-Verlag Heidelberg/Berlin, 1972.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.