die offene Einheitskreisscheibe \({\mathbb{E}}=\{z\in {\mathbb{C}}:|z|\lt 1\}\) zusammen mit der hyperbolischen Metrik \({[.,.]}_{{\mathbb{E}}}\) Der nichteuklidische Abstand zweier Punkte z_i, \({z}_{1},{z}_{2}\in {\mathbb{E}}\) ist dann \({|{z}_{1},{z}_{2}|}_{{\mathbb{E}}}\). Weiter ist die nichteuklidische Länge oder hyperbolische Länge eines rektifizierbaren Weges \(\gamma :[0,1]\to {\mathbb{E}}\) definiert durch \begin{eqnarray}{L}_{h}(\gamma ):=\displaystyle \mathop{\int }\limits_{\gamma }\displaystyle\frac{|dz|}{1-{|z|}^{2}}.\end{eqnarray}

Diese Begriffe lassen sich wie folgt motivieren. Ist \(f\in \,\text{Aut}\,{\mathbb{E}}\)(Automorphismengruppe von \({\mathbb{E}}\)), so gilt \begin{eqnarray}\displaystyle\frac{|{f}{^{\prime} }(z)|}{1-{|f(z)|}^{2}}=\displaystyle\frac{1}{1-{|z|}^{2}}.\end{eqnarray} Hieraus ergibt sich sofort folgender Satz.

Sindz₁, \({z}_{1},{z}_{2},{w}_{1},{w}_{2}\in {\mathbb{E}}\) mit z₁ ≠ z₂ und w₁ ≠ w₂, so existiert ein \(f\in \,\text{Aut}\,{\mathbb{E}}\)mit f (z₁) = w₁und f (z₂) = W₂genau dann, wenn\begin{eqnarray}{[{z}_{1},{z}_{2}]}_{{\mathbb{E}}}={[{w}_{1},{w}_{2}]}_{{\mathbb{E}}}.\end{eqnarray}

Weiter gilt:

Es sei \(\gamma :[0,1]\to {\mathbb{E}}\)ein rektifizierbarer Weg und \(f:\in \,\text{Aut}\,{\mathbb{E}}\)Dann gilt L_h(f o γ) = L_h(γ).

Für den nichteuklidischen Abstand gilt die explizite Formel \begin{eqnarray}\begin{array}{lll}{[{z}_{1},{z}_{2}]}_{{\mathbb{E}}} & = & \displaystyle\frac{1}{2}\, \mathrm{log}\,\displaystyle\frac{|1-{\bar{z}}_{1}{z}_{2}|+|{z}_{1}-{z}_{2}|}{|1-{\bar{z}}_{1}{z}_{2}|-|{z}_{1}-{z}_{2}|}\\ & = & \text{artanh}\left|\displaystyle\frac{{z}_{1}-{z}_{2}}{1-{\bar{z}}_{1}{z}_{2}}\right|,{z}_{1}-{z}_{2}\in {\mathbb{E}}\end{array}\end{eqnarray}

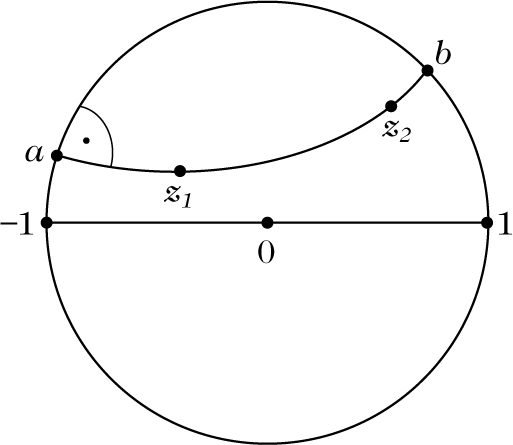
Unter einem Orthokreis in \({\mathbb{E}}\) versteht man einen Durchmesser von \({\mathbb{E}}\) oder einen Kreisbogen in \({\mathbb{E}}\), der zwei Randpunkte \(a,b,\in \partial {\mathbb{E}}\) miteinander verbindet und die Einheitskreislinie senkrecht schneidet.

Damit gilt folgender Satz.

Die kürzeste nichteuklidische Verbindung zweier verschiedener Punkte \({z}_{1},{z}_{2}\in {\mathbb{E}}\)wird durch den zwischen z₁und z₂verlaufenden Bogen des durch z₁und z₂gehenden Ortho kreises gegeben. Die geodätischen Linien der hyperbolischen Metrik sind also die Orthokreise.

Aufgrund dieses Ergebnisses nennt man Orthokreise auch nichteuklidische Geraden und Ortho kreisbögen nichteuklidische Strecken in \({\mathbb{E}}\). Ein Automorphismus von \({\mathbb{E}}\) heißt auch nichteuklidische Bewegung. Für weitere Ausführungen zu dieser Thematik vgl. nichteuklidische Geometrie.

Abschließend sei noch folgender Satz erwähnt.

Es sei f eineholomorphe Funktion in \({\mathbb{E}}\)mit \(f({\mathbb{E}})\subset {\mathbb{E}}.\)Dann gilt\begin{eqnarray}{[f({z}_{1}),f({z}_{2})]}_{{\mathbb{E}}}\le {[{z}_{1},{z}_{2}]}_{{\mathbb{E}}}\end{eqnarray}für alle \({z}_{1},{z}_{2}\in {\mathbb{E}}.\)