Lexikon der Mathematik: α-Niveau-Menge
α-Schnitt, die gewöhnliche Menge
die einer unscharfen Menge à auf X für eine reelle Zahl α ∈ [0, 1] zugeordnet wird.
Die Menge
heißt strenge α-Niveau-Menge (strenger α-Schnitt).
Der Träger supp(Ã) einer unscharfen Menge à ist dann der strenge 0-Schnitt. Die Bedeutung der α-Niveau-Mengen liegt darin, daß die Gesamtheit aller α-Schnitte eine unscharfe Menge à eindeutig bestimmt und umgekehrt, man vergleiche hierzu den Darstellungssatz für unscharfe Mengen.
Einerseits ist es möglich, eine unscharfe Menge in eine Familie von gewöhnlichen Mengen zu zerlegen. Dies wird oft benutzt, um Beziehungen zwischen unscharfen Mengen auf Beziehungen zwischen gewöhnlichen Mengen zurückzuführen.
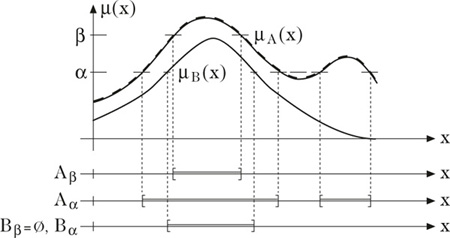
α-Niveau-Mengen
Für unscharfe Mengen
Andererseits erhält man eine unscharfe Menge als obere Einhüllende ihrer Niveau-Mengen. In Anwendungen empfiehlt es sich daher, eine endliche Teilmenge L ⊂ [0, 1] relevanter Zugehörigkeitsgrade auszuwählen, für diese dann die zugehörigen Niveau-Mengen festzulegen und die unscharfe Menge à durch das Mengensystem
zu beschreiben, das für α, β ∈ L den Konsistenzbedingungen
genügen muß.
In praktischen Anwendungen reichen im allgemeinen wenige Niveau-Mengen aus, um eine unscharfe Menge hinreichend genau näherungsweise zu beschreiben.
Es muß allerdings darauf geachtet werden, daß die ausgewählten Zugehörigkeitsgrade über das Intervall [0, 1] verteilt und inhaltlich interpretierbar sind (Fuzzy-Intervalle vom ϵ-λ-Typ).
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.