auch Niveaumenge oder Äquipotentialfläche, Gesamtheit aller Punkte \begin{eqnarray}\{x\in {\mathfrak{D}}|\varphi (x)=c\}\end{eqnarray} für \({\mathfrak{D}}\subset {{\mathbb{R}}}^{n},\varphi :{\mathfrak{D}}\to {\mathbb{R}},{\mathbb{R}}\,{\unicode {8717}}\,c\) und n ∈ ℕ; den Wert c bezeichnet man als das Niveau.

Für n = 3 ist dies gerade die Gesamtheit der Punkte (Fläche) im Raum, auf der ein gegebenes Skalarfeld \(\varphi :{\mathfrak{D}}\to {\mathbb{R}}\) einen konstanten Wert annimmt.

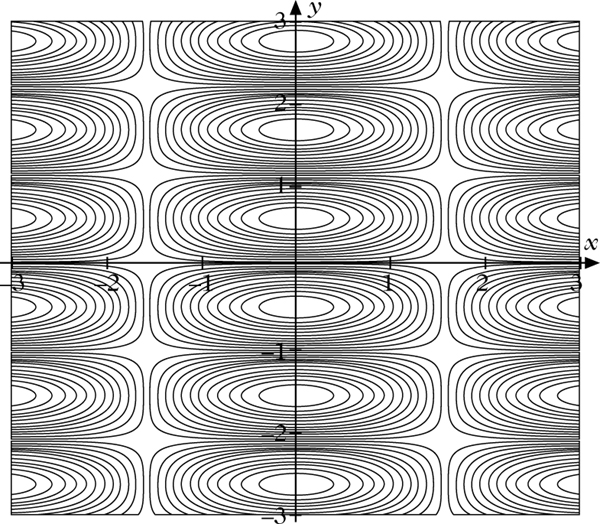
Im ℝ² entsprechen diesen die Niveaulinien oder Höhenlinien, wie sie von geographischen Karten her vertraut sind. Auch die Isobare auf der Wetterkarte sind ein oft gesehenes Beispiel. In Anwendungen haben die Höhenlinien oft spezielle Namen, so etwa in den Wirtschaftswissenschaften „Isoquanten“ bei Produktionsfunktionen, „Isokostenlinie“ bei Kostenfunktionen und „Indifferenzkurve“ bei Nutzenfunktionen.