Lexikon der Mathematik: Normalgleichung
die Gleichung ATAx = ATb, deren Lösung x gerade die Lösung des in der Ausgleichsrechnung häufig anzutreffenden linearen Ausgleichsproblems
ist.
Da ATA eine symmetrische Matrix ist kann die Normalgleichung mittels des Cholesky-Verfahrens gelöst werden. Bei der Lösung der Normalgleichung können numerische Probleme auftreten, wenn die Konditionszahl der Matrix ATA sehr groß ist. Die Lösung x hat dann relativ große Fehler. Zudem sind Rundungsfehler bereits bei der Berechnung von ATA und ATb unvermeidlich. Man sollte das lineare Ausgleichsproblem daher mittels der QR-Zerlegung lösen. Dieses Verfahren wird unter Methode der kleinsten Quadrate beschrieben.
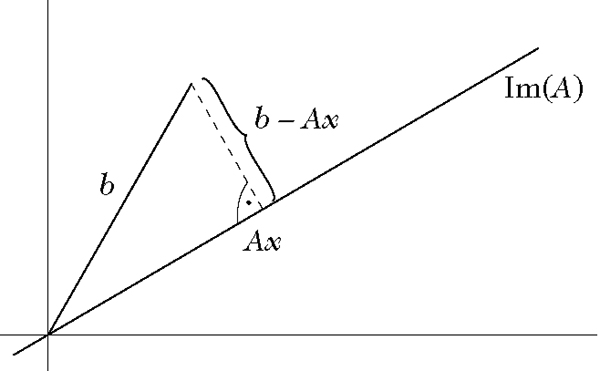
b − Ax ist Normale auf Im(A)
Geometrisch besagt die Normalgleichung, daß b − Ax eine Normale auf Im(A) ∪ ℝm ist. Dies gibt ihr den Namen.
Bei der Lösung eines nichtlinearen Ausgleichsproblems
liefern die Normalgleichungen
die notwendige Bedingung für ein Minimum des obigen Ausdrucks.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.