Gaußsche Normalverteilung, Gauß-Verteilung, das zu den reellen Parametern μ und σ², σ > 0, durch die Wahrscheinlichkeitsdichte \begin{eqnarray}{f}_{\mu,{\sigma }^{2}}:{\mathbb{R}}{\unicode {x0220D}}x\to \frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^{2}}\in {{\mathbb{R}}}^{+}\end{eqnarray}

definierte Wahrscheinlichkeitsmaß.

Die Normalverteilung mit Parametern μ und σ² wird in der Regel kurz als N(μ, σ²)-Verteilung bezeichnet. Die N(0, 1)-Verteilung heißt Standardnormalverteilung. Die Werte ihrer Verteilungsfunktion Φ berechnet man approximativ mit dem Computer oder entnimmt sie Tabellenwerken. Diese Tabellenwerke enthalten in der Regel nur die Werte Φ(x) für Argumente x ≥ 0. Für negative Argumente berechnet man den Wert der Verteilungsfunktion unter Ausnutzung der Symmetriebeziehung Φ(x) = 1 − Φ(−x), welche für alle x ∈ ℝ gilt.

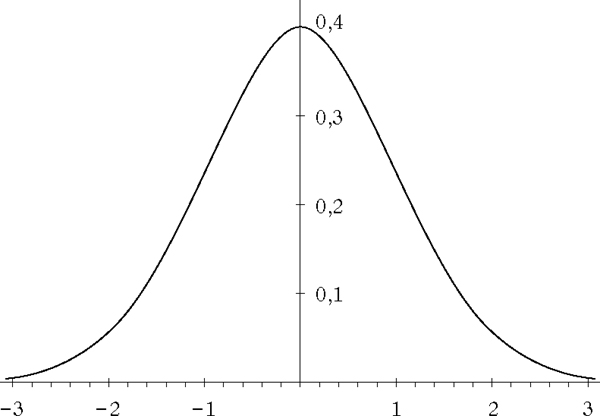
Die Dichte f_{μ, σ²} ist achsensymmetrisch zur Achse x = μ, besitzt an der Stelle μ einen eindeutig bestimmten Modalwert, und Wendepunkte an den Stellen μ ± σ. Ihr Graph wird als „Gaußsche Glockenkurve“ bezeichnet.

Die Normalverteilung ist eine stabile und folglich auch unbegrenzt teilbare Verteilung. Besitzt die auf dem Wahrscheinlichkeitsraum (Ω, 𝔄, P) definierte Zufallsvariable X eine N(μ, σ²)-Verteilung, so gilt für den Erwartungswert E(X) = μ und für die Varianz Var(X) = σ². Die Zufallsvariable (X − μ)/σ besitzt dann eine Standardnormalverteilung, sodaß insbesondere für die Verteilungsfunktion Φ_{μ, σ²} von X die Beziehung \begin{eqnarray}{\Phi }_{\mu,{\sigma }^{2}}(x)=\Phi \left(\frac{x-\mu }{\sigma }\right)\end{eqnarray}

für alle x ∈ ℝ gilt. Innerhalb der Intervalle mit den Endpunkten μ ± σ, μ ± 2σ und μ ± 3σ nimmt X Werte mit den Wahrscheinlichkeiten P(|X − μ| ≤ σ) ≈ 0, 6827, P(|X − μ| ≤ 2σ) ≈ 0, 9545 und P(|X − μ| ≤ 3σ) ≈ 0, 9973 an.

Sind X₁ und X₂ unabhängige, nicht notwendig mit den gleichen Parametern normalverteilte Zufallsvariablen, so ist auch die Summe X₁ + X₂ normalverteilt.

Ihre besondere Bedeutung für die Wahrscheinlichkeitstheorie und die Statistik verdankt die Normalverteilung u. a. dem zentralen Grenzwertsatz. Die mehrdimensionale Verallgemeinerung der Normalverteilung bezeichnet man als multivariate Normalverteilung.