auch numerische Quadratur bzw. Kubatur, Methoden der näherungsweise Berechnung von Integralen.

In der numerischen Integration wird – im eindimensionalen Fall – das bestimmte Integral \begin{eqnarray}\displaystyle \underset{a}{\overset{b}{\int }}f(t)dt\end{eqnarray}

näherungsweise durch eine Integrationsformel (auch: Quadraturformel) \begin{eqnarray}{Q}_{n}(f)=\displaystyle \sum _{i=0}^{n-1}{a}_{i}f({x}_{i})\end{eqnarray}

berechnet. Dies wird notwendig, wenn sich eine Stammfunktion von f nicht durch elementare Funktionen ausdrücken läßt, die numerische Auswertung der Stammfunktion zu komplex ist oder der Integrand nur diskret, etwa als Ergebnis von Messungen, vorliegt.

Eine Möglichkeit, solche Näherungsformeln zu bestimmen, ergibt sich aus fortgesetzter Newton-Cotes Quadratur. Hierbei geht man von einer äquidistanten Intervallunterteilung x_i = a + ih, i = 0, \(h=\frac{b-a}{n-1}\), aus, und nähert den Integranden stückweise durch interpolierende Polynome eines festen Grades m.

Eine einfache Möglichkeit hierfür ist es, die Funktion f in jedem der Intervalle (x_i−1, x_i), i = 1, …, n − 1, durch eine Konstante y_i−1 = f (ξ_i−1) mit ξ_i−1 ∈ [x_i−1, x_i] zu nähern, d. h. m = 0. In diesem Fall erhält man die Rechtecks-Regel \begin{eqnarray}{Q}_{n}^{(0)}(f)=h\displaystyle \sum _{i=0}^{n-2}{y}_{i}.\end{eqnarray}

Im Spezialfall \({\xi }_{i-1}=\frac{{x}_{i-1}+{x}_{i}}{2}\) heißt die Rechtecks-Regel auch Mittelpunkts-Regel.

Fehlerabschätzungen (in der numerischen Integration) hängen im allgemeinen von der Gutartigkeit von f ab. Ist f eine stetige Funktion auf [a, b], so ergibt sich die Fehlerabschätzung \begin{eqnarray}\left|\displaystyle \underset{a}{\overset{b}{\int }}f(t)dt-{Q}_{n}^{(0)}(f)\right|\le \omega (f,h)(b-a),\end{eqnarray}

wobei \begin{eqnarray}\omega (f,h)=\max \{|f(x)-f(y)|:|x-y|\lt h\}\end{eqnarray}

der Stetigkeitmodul von f ist. Für die Mittelpunkts-Regel gilt \begin{eqnarray}\left|\displaystyle \underset{a}{\overset{b}{\int }}f(t)dt-{Q}_{n}^{(0)}(f)\right|\le \omega (f,\frac{h}{2})(b-a)\end{eqnarray}

und, falls f eine zweimal differenzierbare Funktion auf [a, b] ist: \begin{eqnarray}\left|\displaystyle \underset{a}{\overset{b}{\int }}f(t)dt-{Q}_{n}^{(0)}(f)\right|\le \frac{{h}^{2}}{24}\mathop{\max }\limits_{x\in [a,b]}|{f}^{\prime\prime}(x)|(b-a).\end{eqnarray}

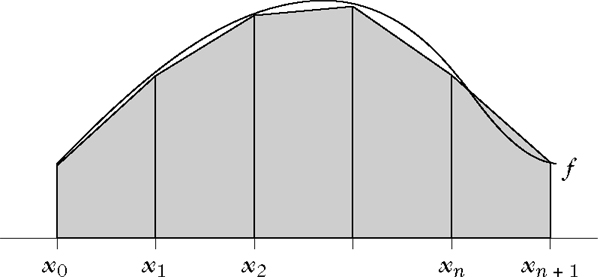
Interpoliert man die Funktion f an den Stellen y_i−1 = f(x_i−1), i = 1, …, n, über den Intervallen [x_i−1, x_i] jeweils linear, so ergibt sich die Trapezregel (auch: Sehnentrapezregel) \begin{eqnarray}{Q}_{n}^{(1)}(f)=h\left(\frac{{y}_{0}}{2}+\displaystyle \sum _{i=1}^{n-2}{y}_{i}+\frac{{y}_{n-1}}{2}\right).\end{eqnarray}

Durch Schrittweitenextrapolation wird die Konvergenz solcher Quadraturformeln verbessert. Diese Vorgehensweise nennt man Romberg-Verfahren.

Eine weitere Methode der numerischen Integration stammt von Gauß. Nach dieser Vorgehensweise werden nicht nur die Gewichte a_i, sondern auch die Stützstellen x_i als Parameter von Q_n(f) aufgefaßt. Die Gaußsche Quadraturformel erhält man durch die Forderung, daß für alle Polynome bis zum maximalen Grad 2n − 1 \begin{eqnarray}\displaystyle \underset{a}{\overset{b}{\int }}p(t)dt={Q}_{n}(p)\end{eqnarray}

gilt. Ist [a, b] = [−1, 1], so bilden die Nullstel len x₀, …, x_n−1 ∈ (−1, 1) des n-ten Legendre-PolynomsL_n eine geeignete Wahl von Stützstellen. Die zugehörigen Gewichte berechnen sich als \begin{eqnarray}{a}_{i}=\displaystyle \underset{-1}{\overset{1}{\int }}{l}_{i}(t)dt,\end{eqnarray}

wobei l_i, i = 0, …, n − 1, das i-te Lagrange-Polynom vom Grad n − 1 ist. Dies ergibt sich aus der Orthogonalitätseigenschaft der Legendre-Polynome.

Für den Fehler der Gauß-Quadratur hinsichtlich einer 2n-fach differenzierbaren Funktion f auf [−1, 1] gilt \begin{eqnarray}\displaystyle \underset{a}{\overset{b}{\int }}f(t)dt-{Q}_{n}(f)=\frac{{2}^{2n+1}n{!}^{4}}{{(2n!)}^{3}(2n+1)}{f}^{(2n)}(\xi )\end{eqnarray}

wobei ξ ∈ (−1, 1).

Allgemeiner werden Quadraturformeln vom Gaußschen Typ verwendet, um (uneigentliche) Integrale der Form \begin{eqnarray}\displaystyle \int \omega (t)f(t)dt\end{eqnarray}

zu nähern. Hierbei ist ω eine Gewichtsfunktion mit der Eigenschaft ω(t) > 0. Beispielsweise sind die Nullstellen der Tschebyschew-Polynome die Stützstellen bzgl. der Gewichtsfunktion \(\omega (t)={(1-{t}^{2})}^{-{\scriptstyle \frac{1}{2}}}\) im Intervall (−1, 1). Im Intervall [0, ∞) bilden die Nullstellen der Laguerre-Polynome die Stützstellen bzgl. der Gewichtsfunktion ω(t) = exp(−t).

Prinzipiell analoge, allerdings durch die höhere Dimension und Anzahl der Freiheitsgrade wesentlich kompliziertere Zugänge und Formeln existieren auch für höherdimensionale Integrale. Hierbei spricht man von (Numerischer) Kubatur, während für den oben behandelten eindimensionalen Fall auch die Bezeichnung (Numerische) Quadratur benutzt wird.

Eine schöne Darstellung der hier aus Platzgründen nicht weiter behandelten Kubaturformeln findet man in [1] und [2].

[1] Davis, P.J.; Rabinowitz, P.: Methods of numerical integration. Academic Press Orlando, 1980.
[2] Engels, H.: Numerical quadrature and cubature. Academic Press Orlando, 1984.
[3] Hämmerlin, G; Hoffmann, K.-H.: Numerische Mathematik. Springer-Verlag Berlin/Heidelberg, 1991.
[4] Meinardus, G.; Merz, G.: Praktische Mathematik I. BI-Wissenschaftsverlag Mannheim, 1979.
[5] Stoer, J.: Einführung in die Numerische Mathematik I. Springer-Verlag Berlin/Heidelberg, 1972.