das für eine auf dem Träger (\({\mathfrak{F}}\)) eines regulären Flächenstücks \({\mathfrak{F}}\) definierte reellwertige Funktion f durch \begin{eqnarray}\begin{array}{cc}\displaystyle \mathop{\iint }\limits_{{\mathfrak{F}}}f\,d\omega :=\displaystyle \mathop{\iint }\limits_{K}f\circ {\rm{\Phi }}(u,w)\,d\omega\end{array}\end{eqnarray} mit \begin{eqnarray}d\omega =\Vert {D}_{1}{\rm{\Phi }}(\,\,)\times {D}_{2}{\rm{\Phi }}(\,\,)\Vert \,d(u,v)\end{eqnarray} definierte Integral. Hierbei seien K eine geeignete kompakte Teilmenge des ℝ² und Φ : K → ℝ³ eine Parameterdarstellung von \({\mathfrak{F}}\), also \begin{eqnarray}({\mathfrak{F}}):={\rm{\Phi }}(K).\end{eqnarray}

Dazu ist zunächst – analog zur Kurventheorie – der Inhalt geeigneter Flächen im ℝ³ zu definieren. Dies sei hier nur skizziert. Genauer und wesentlich allgemeiner wird der Sachverhalt in mathematischen Darstellungen der Vektoranalysis ausgeführt. Es sei stets ║ ║ ≔ ║ ║₂, also die euklidische Norm, betrachtet.

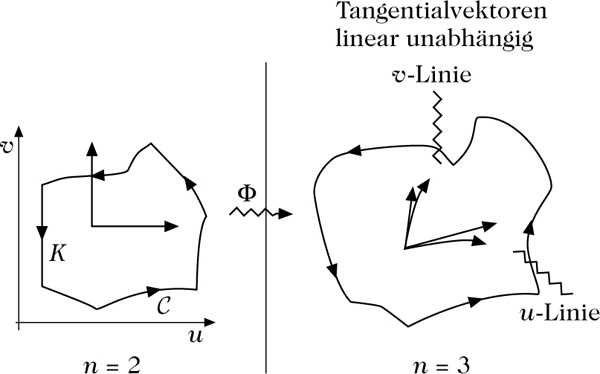
Ein „reguläres Flächenstück“ wird über eine ‚Parameterdarstellung‘ wie folgt definiert: Es seien ℝ² ⊃ K kompakt; der Rand ∂K von K sei (\(\mathfrak{C}\)) mit einer stetigen, stückweise glatten, geschlossenen, doppelpunktfreien Kurve \(\mathfrak{C}\). (K ist dann eine zwei-dimensionale Jordan-Menge.)

Es sei als Beispiel die Oberfläche einer Kugel vom Radius r > 0 berechnet. Hier ist \begin{eqnarray}{\rm{\Phi }}(\vartheta,\varphi ):=\left(\begin{array}{c}r\cos \vartheta \cos \varphi \\ r\cos \vartheta \sin \varphi \\ r\sin \vartheta \end{array}\right)\,\,\,\,\,\,(\vartheta \in [-\frac{\pi }{2},\frac{\pi }{2}],\,\,\varphi \in [0,2\pi ])\end{eqnarray}\begin{eqnarray}{{\mathfrak{r}}}_{\vartheta }=r(\begin{array}{c}-\sin \vartheta \cos \varphi \\ -\sin \vartheta \sin \varphi \\ \cos \vartheta \end{array}),{{\mathfrak{r}}}_{\varphi }=r(\begin{array}{c}-\cos \vartheta \sin \varphi \\ \cos \vartheta \cos \varphi \\ 0\end{array})\end{eqnarray}\begin{eqnarray}{g}_{11}=E={r}^{2},{g}_{22}=G={r}^{2}{(\cos \vartheta )}^{2},{g}_{12}=F=0\\ \Vert {{\mathfrak{r}}}_{\vartheta }\times {{\mathfrak{r}}}_{\varphi }\Vert ={r}^{2}\cos \vartheta. \end{eqnarray}

(Die obigen Voraussetzungen sind, da cos ϑ = 0 für \(\vartheta =\pm \frac{\pi }{2}\), nicht auf dem ganzen Bereich gegeben! Man betrachtet geeignete Teilmengen und macht dann einen Grenzubergang.) Es folgt \begin{eqnarray}\omega ({\mathfrak{F}})=\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\displaystyle \underset{0}{\overset{2\pi }{\int }}{r}^{2}\cos \vartheta \,d\varphi \,d\vartheta =4\pi {r}^{2}.\end{eqnarray}

Die Überlegungen zum Oberflächeninhalt motivieren nun, über Näherungssummen der Art \begin{eqnarray}\displaystyle \sum _{\text{endlich}}f({P}_{v})\omega ({{\mathfrak{F}}}_{v}),\end{eqnarray} die schon zu Beginn angegebene Definition (1).