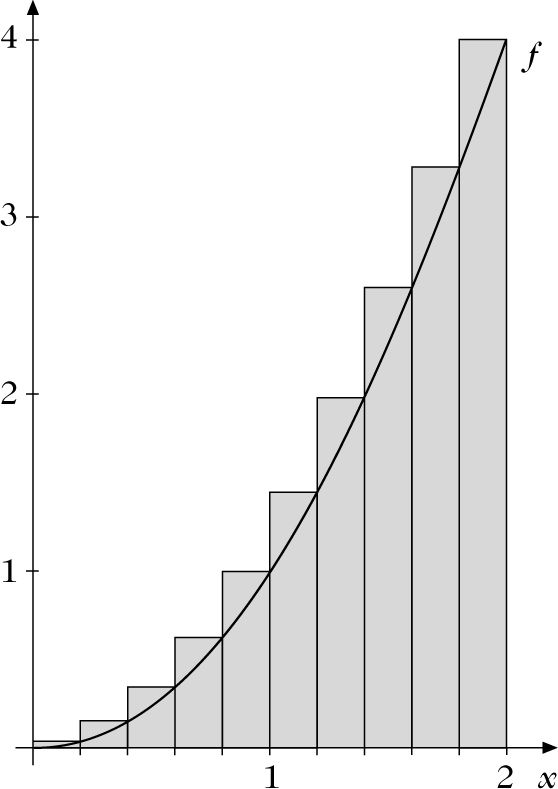
Integral einer majorisierenden Treppenfunktion (Oberfunktion) zu einer vorgegebenen (beschränkten) Funktion \begin{eqnarray}f:[a,b]\to {\mathbb{R}},\end{eqnarray} wobei a, b ∈ ℝ mit a < b. Mit einer Zerlegung \begin{eqnarray}a={x}_{0}\lt {x}_{1}\lt \cdots \lt {x}_{n}=b\end{eqnarray} und Werten α_v (v = 0, …, n − 1) mit \begin{eqnarray}f(x)\le {\alpha }_{v}\,\,\,\,\text{f}\mathrm{\ddot{u}}\text{r}\,\,\,\,{x}_{v}\le x\le {x}_{v+1}\end{eqnarray} ist eine Obersumme also eine Summe der Art \begin{eqnarray}\displaystyle \sum _{v=0}^{n-1}{a}_{v}({x}_{v+1}-{x}_{v})\end{eqnarray} (Summe von Rechtecksinhalten).

Bei fester Zerlegung der o.a. Art ist die optimale (kleinste) Obersumme offenbar gegeben durch \begin{eqnarray}{\alpha }_{v}:=\sup \{f(x)|{x}_{v}\le x\le {x}_{v+1}\}.\end{eqnarray}

Gelegentlich wird auch nur dieser spezielle Wert als Obersumme bezeichnet.

Das Infimum über alle Obersummen (zu f) bezeichnet man auch als oberes Darboux-Integral und notiert dafür auch b \begin{eqnarray}\displaystyle \underset{a}{\overset{\underline {b}}{\int }}f(x)\,dx.\end{eqnarray}