Lexikon der Mathematik: Ordnungsrelation
Ordnung, geordnetes Paar (M, R), so daß (M, M, R), R ⊆ M × M, eine Relation darstellt, die den folgenden drei Bedingungen genügt (wie üblich wird im folgenden für zwei in Relation stehende Elemente x, y die Bezeichnung x ~ y anstatt (x, y) ∈ R verwendet):
1. Reflexivität:
2. Antisymmetrie:
3. Transitivität:
Eine Abschwächung des Begriffes der Ordnungsrelation ist der Begriff der Partialordnung, Halbordnung oder partiell geordneten Menge. Hier wird lediglich verlangt, daß die Relation R reflexiv und transitiv ist. Man beachte, daß es in der Literatur auch vorkommt, daß der hier als Ordungsrelation definierte Begriff als Partialordnung oder als Halbordnung bezeichnet wird.
R heißt strenge Ordnungsrelation genau dann, wenn R transitiv und asymmetrisch ist. Dabei heißt R genau dann asymmetrisch, wenn
Eine Ordnungsrelation und eine strenge Ordnungsrelation unterscheiden sich genau durch die Diagonale
Für Ordnungsrelationen und Partialordnungen ist es üblich, das Symbol „≤“ (lies: „kleiner oder gleich“) anstatt des Symbols „~“ zu verwenden. Im Fall strenger Ordnungsrelationen wird das Symbol „<“ (lies: „kleiner“ oder „echt kleiner“) benutzt.
Beispiel: Es sei \({\mathcal{M}}:={\mathcal{P}}({{\mathbb{N}}}_{0})\) die Potenzmenge der natürlichen Zahlen. Durch
Eine Partialordnung (M, ≤) läßt sich häufig in einem Ordnungsdiagramm (gelegentlich auch Hasse-Diagramm genannt) veranschaulichen. Dabei werden die Elemente der partiell geordneten Menge M als Punkte der Zeichenebene dargestellt, für a ≤ b wird a unterhalb oder auf gleicher Höhe von b gezeichnet, und a wird mit b verbunden. Der Übersichtlichkeit halber ist es üblich, Punkte nicht zu verbinden, wenn sie schon über andere Punkte verbunden sind.
Stellt ein Ordnungsdiagramm eine Partialordnung dar, so werden i. allg. waagrechte Linien auftreten. In Veranschaulichungen von Ordnungsrelationen lassen sich waagrechte Linien hingegen vermeiden, wenn man für verschiedene Elemente a, b mit a ≤ b den Punkt a immer unterhalb des Punktes b zeichnet.
Beispiele:
1. In Abbildung 1 ist ein Ordnungsdiagramm der durch Inklusion geordneten Menge \(\{{\mathbb{N}},\,{{\mathbb{Z}}}^{-},\,{\mathbb{Z}},\,{{\mathbb{Q}}}^{-},\,{\mathbb{Q}},\,{\mathbb{R}},\,{\mathbb{A}}\text{,}\,{\mathbb{C}}\}\) dargestellt.
Abbildung 1
2. Man betrachte die Menge
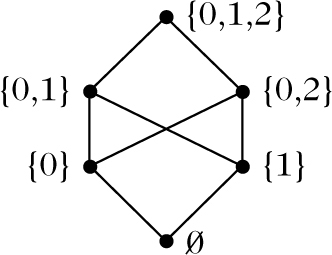
Dann wird genau wie oben durch M ≤ N :⇔ #M ≤ #N eine Partialordnung auf \( {\mathcal M} \) definiert. Abbildung 2 liefert die Veranschaulichung in einem Ordnungsdiagramm.
Abbildung 2
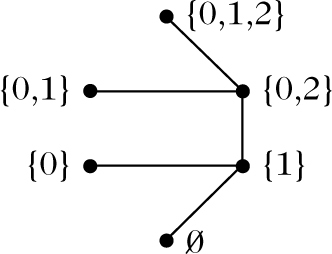
3. Analog zu oben kann man auf \( {\mathcal M} \) eine Ordnungsrelation „≤0“ definieren durch M ≤0N genau dann, wenn M = N oder #M< #N. Das zugehörige Ordnungsdiagramm zeigt Abbildung 3.
Abbildung 3
Sind M1, M2 mit den Partialordnungen „≤1“ bzw. „≤2“ versehene Mengen, so heißt eine Abbildungf : M1 → M2 isoton genau dann, wenn für alle x, y ∈ M1 aus x ≤1y folgt, daß f (x) ≤2f (y).
Eine Abbildung f : M1 → M2 heißt antiton genau dann, wenn für alle x, y ∈ M1 aus x ≤1y folgt, daß f(y) ≤2f(x).
Für die Definition streng isotoner bzw. streng antitoner Abbildungen sind in der Definition isotoner bzw. antitoner Abbildungen die Partialordnungen „≤1“ und „≤2“ durch strenge Ordnungsrelationen „≤1“ und „≤2“ zu ersetzen.
Die Abbildung f heißt genau dann ähnlich oder ordnungstreu, wenn f bijektiv ist und sowohl f als auch f−1 isoton sind. In diesem Fall werden auch die Partialordnungen (M1, ≤1) und (M2, ≤2) bzw. die partiell geordneten Mengen M1 und M2 ähnlich genannt.
Beispiele:
4. Betrachtet man die in den Abbildungen 3 bzw. 2 dargestellten Partialordnungen \(( {\mathcal M} \text{,}{\le }_{o})\) und \(( {\mathcal M} \text{,}\le )\), so ist die Identität auf \( {\mathcal M} \) isoton, jedoch nicht ähnlich, da die Umkehrabbildung nicht isoton ist (da z. B. {1} ≤ {0}, jedoch nicht {1} ≤0 {0}).
5. Die Abbildung f : ℝ → ℝ, x ↦ mx + n, ist isoton genau dann, wenn m ≥ 0, antiton genau dann, wenn m ≤ 0, streng isoton sowie ähnlich genau dann, wenn m > 0, und streng antiton genau dann, wenn m< 0.
(M, ≤) wird nun als Partialordnung vorausgesetzt. Man spricht von Vergleichbarkeit der Elemente x, y ∈ M genau dann, wenn x ≤ y oder y ≤ x gilt, und von Kompatibilität der Elemente x, y ∈ M genau dann, wenn es ein Element z ∈ M mit z ≤ x und z ≤ y gibt.
Der Begriff der Kompatibilität ist stärker als der der Vergleichbarkeit: Sind zwei Elemente vergleichbar, so sind sie auch kompatibel; die Umkehrung gilt jedoch i. allg. nicht. So sind ℚ− und ℤ in Abbildung 1 kompatibel, jedoch nicht vergleichbar.
Eine Menge K ⊆ M heißt Kette genau dann, wenn alle Elemente aus K paarweise im oben definierten Sinne vergleichbar sind.
Eine Menge A ⊆ M heißt Antikette genau dann, wenn je zwei verschiedene Elemente aus A nicht kompatibel sind.
In Abbildung 1 ist z. B. die Menge \(\{{{\mathbb{Z}}}^{-},\,{\mathbb{Z}},\,{\mathbb{Q}},\,{\mathbb{A}}\}\) eine Kette und die Menge {ℤ−, ℕ} eine Antikette. Ein weiteres Beispiel für eine Kette ist die zur Abbildung 2 gehörige Menge \( {\mathcal M} \).
Die abzählbare Kettenbedingung für die Partialordnung (M, ≤) ist die Aussage, daß jede Antikette A ⊆ M abzählbar ist.
Beispiel: Ist X eine Menge und M die Potenzmenge von X, aus der die leere Menge entfernt wurde, d. h., \(M={\mathcal{P}}(M)\backslash \{\emptyset \}\), und ist M durch die Inklusion von Mengen geordnet, so sind zwei Elemente aus M genau dann kompatibel, wenn sie nicht disjunkt sind. Somit erfüllt (M, ⊆) genau dann die abzählbare Kettenbedingung, wenn die Menge X abzählbar ist.
Eine Menge D ⊆ M heißt dicht in M genau dann, wenn es zu jedem x ∈ M ein Element d ∈ D mit d ≤ x gibt.
Beispiele: In Abbildung 1 ist eine Menge genau dann dicht, wenn sie die Elemente ℤ− und ℕ enthält. In den Abbildungen 2 und 3 ist eine Menge genau dann dicht, wenn sie das Element ∅ enthält. ℤ ist eine dichte Teilmenge der reellen Zahlen mit der üblichen Ordnung.
Eine Menge F ⊆ M heißt Filter auf M genau dann, wenn die folgenden Bedingungen (i) und (ii) erfüllt sind:
Beispiele:
6. In Abbildung 1 ist die Menge \(\{{\mathbb{C}},{\mathbb{R}},{\mathbb{A}}\}\) kein Filter. Einen Filter erhält man, indem man der Menge das Element ℚ hinzufügt.
7. In Abbildung 2 ist die Menge {{1}, {0,2}, {0, 1, 2}} kein Filter. Einen Filter erhält man, indem man der Menge die Elemente {0} und {0, 1} hinzufügt.
8. ℕ ist ein Filter auf ℤ mit der üblichen Ordnung.
9. Ist M eine Menge und \(F\subseteq {\mathcal{P}}(M)\) ein Filter über M, so ist F ein Filter auf der Ordnungsrelation \(({\mathcal{P}}(M),\subseteq )\).
Ein Element m ∈ M heißt größtes Element genau dann, wenn für alle x ∈ M gilt x ≤ m · m heißt maximales Element genau dann, wenn für jedes x ∈ M aus m ≤ x folgt, daß x = m ist. m heißt kleinstes Element genau dann, wenn für alle x ∈ M gilt m ≤ x ist. m heißt minimales Element genau dann, wenn für jedes x ∈ M aus x ≤ m folgt, daß x = m.
Ist N ⊆ M, so heißt s ∈ M obere Schranke von N genau dann, wenn n ≤ s für alle n ∈ N gilt. N heißt dann nach oben beschränkt. Analog heißt s ∈ M untere Schranke von N genau dann, wenn s ≤ n für alle n ∈ N gilt. N heißt dann nach unten beschränkt. Ein kleinstes Element der Menge der oberen Schranken der Menge N heißt Supremum oder obere Grenze der Menge N und wird mit sup(N) bezeichnet. Entsprechend heißt ein größtes Element der Menge der unteren Schranken der Menge N Infimum oder untere Grenze der Menge N und wird mit inf(N) bezeichnet. Sofern das Supremum bzw. das Infimum existiert, ist es eindeutig bestimmt.
Beispiele:
10. Die in Abbildung 1 dargestellte Ordnungsrelation hat ℂ als größtes Element. Sie hat kein kleinstes Element, jedoch zwei minimale Elemente, nämlich ℤ− und ℕ. Ist \(T:=\{{\mathbb{Z}},\,{\mathbb{Q}},\,{\mathbb{R}},\,{\mathbb{A}}\text{,}\,{\mathbb{C}}\}\), so sind ℤ−, ℕ und ℤ untere Schranken von T, d. h., T ist nach unten beschränkt. Es gilt inf(T) = ℤ. T ist auch nach oben beschränkt, und es gilt sup(T) = ℂ. Die Menge {ℤ−, ℕ} ist nicht nach unten beschränkt.
11. Die Menge \({{\mathbb{Q}}}_{0}^{+}\) hat 0 als kleinstes Element, sie hat kein größtes Element und ist nicht nach oben beschränkt. Die Menge (1, \(\sqrt{2]}\,\cap {\mathbb{Q}}\) ist in \({{\mathbb{Q}}}_{0}^{+}\) sowohl nach oben als auch nach unten beschränkt, sie hat 1 als Infimum, jedoch kein Supremum.
12. Betrachtet man die Menge
Nun wird (M, ≤) als Ordnungsrelation vorausgesetzt.
Die zu „≤“ inverse Ordnungsrelation wird mit „≥“ bezeichnet, d.h., es gilt a ≥ b genau dann, wenn b ≤ a.
Ist N ⊆ M und gilt x ≤N y für x, y ∈ N genau dann, wenn x ≤ y, so bezeichnet man (N, ≤N) als Teilordnung von (M, ≤).
Sind a, b ∈ M, a ≤ b, a ≠ b, so heißt b ein Nachfolger von a genau dann, wenn für jedes c ∈ M aus a ≤ c ≤ b entweder c = a oder c = b folgt.
Beispiele: In Abbildung 1 hat jedes Element außer ℂ mindestens einen Nachfolger. ℤ− und ℚ besitzen zwei Nachfolger. Bezüglich der üblichen Ordnungen hat jedes Element von ℤ genau einen Nachfolger, jedoch hat kein Element von ℚ oder ℝ einen Nachfolger.
Man spricht bei (M, ≤) genau dann von einer linearen, konnexen, totalen oder vollständigen Ordnungsrelation und bezeichnet M als linear, konnex, total oder vollständig geordnet, wenn für alle a, b ∈ M gilt, daß a ≤ b oder b ≤ a.
Beispiele für lineare Ordnungsrelationen sind ℕ, ℤ, ℚ und ℝ mit den üblichen Ordnungen.
M heißt induktiv geordnet genau dann, wenn jede durch „≤“ linear geordnete Teilmenge von M ein Supremum besitzt.
Keine der Mengen ℕ, ℤ, ℚ und ℝ mit den üblichen Ordnungen ist induktiv geordnet. Hingegen ist ℤ− induktiv geordnet. Ebenso sind alle abgeschlossenen reellen Intervalle sowie halboffene reelle Intervalle der Form (a, b] mit b ∈ ℝ, a ∈ ℝ ∪ {∞}, a< b, induktiv geordnet. Das obige Beispiel 11 zeigt, daß die Menge [0, 2] ∩ ℚ nicht induktiv geordnet ist. Die Menge aller linear unabhängigen Teilmengen eines Vektorraumes mit der Inklusion als Ordnung ist indukiv geordnet.
Ist M linear geordnet, so heißt A ⊆ M Abschnitt genau dann, wenn A genau alle Elemente enthält, die echt kleiner einem gegebenen Element x ∈ M sind.
Beispiele: Die Abschnitte der reellen Zahlen sind genau die offenen Intervalle (∞, a) mit a ∈ ℝ. Jede Ordinalzahl ist die Menge ihrer Abschnitte (Kardinalzahlen und Ordinalzahlen).
Ist die Menge M1 durch „≤1“ und die Menge M2 durch „≤2“ geordnet, so läßt sich wie folgt eine Ordnung „≤“ auf M1 × M2 definieren: Für a1, b1 ∈ M1 und a2, b2 ∈ M2 sei (a1, a2) ≤ (b1, b2) genau dann, wenn entweder a1 ≤ b1, a1 ≠ b1 oder a1 = b1, a2 ≤ b2. (M1 × M2, ≤) wird dann als lexikographisches Produkt von (M1, ≤1) und (M2, ≤2) bezeichnet.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.