unendlich ausgedehnte Kurve zweiter Ordnung.

I. Funktionsgraphen von quadratischen Funktionen f mit f(x) = ax² + bx + c (mit a ≠ 0) sind Parabeln, für den speziellen Fall f(x) = x² spricht man auch von der Normalparabel, wobei die an deren Parabeln durch Ähnlichkeitsabbildungen aus der Normalparabel hervorgehen.

II. Parabel als Kegelschnitt. Eine Parabel ist Schnittfigur einer Ebene ϵ und eines Doppelkegels K, wobei ϵ nicht durch die Spitze von K verlaufen darf, und der Winkel β zwischen ϵ und der Kegelachse gleich dem halben Öffnungswinkel α des Kegels sein muß (Kegelschnitt).

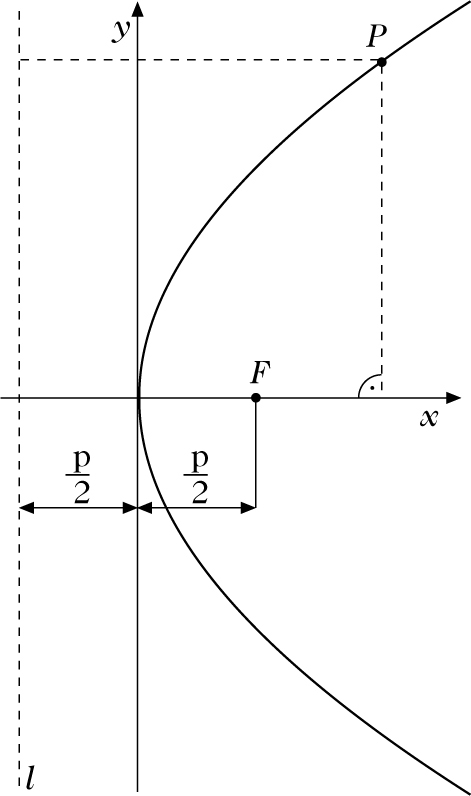
III. Ortsdefinition der Parabel. Eine Parabel ist die Menge aller Punkte P einer Ebene, für die der Abstand von einem festen Punkt F gleich dem Abstand von einer festen Geraden l ist: \begin{eqnarray}|PF|=d(P,l).\end{eqnarray}

Der Punkt F wird als Brennpunkt, die Gerade l als Leitlinie der Parabel bezeichnet. Der Abstand p des Brennpunktes von der Leitlinie heißt Halbparameter der Parabel. Die zur Leitlinie l senkrechte Gerade durch den Brennpunkt wird Achse, und der Schnittpunkt einer Parabel mit ihrer Achse Scheitelpunkt der Parabel genannt.

IV. Gleichungen der Parabel. Wird ein Koordinatensystem bezüglich einer gegebenen Parabel so gewählt, daß die x–Achse mit der Parabelachse und der Koordinatenursprung mit ihrem Scheitel übereinstimmt (die y–Achse verläuft dann parallel zur Leitlinie), so läßt sich die Parabel durch die sogenannte Scheitelgleichung \begin{eqnarray}{y}^{2}=2p\,x\end{eqnarray} beschreiben. Verläuft die x–Achse parallel zur Parabelachse, und hat der Brennpunkt die Koordinaten (x₀, y₀), so erhält man als Parabelgleichung in achsenparalleler Lage \begin{eqnarray}{(y-{y}_{0})}^{2}=2p(x-{x}_{0}).\end{eqnarray}

In einem Polarkoordinatensystem, dessen Pol der Brennpunkt der gegebenen Parabel ist, läßt sich diese durch die folgende Polargleichung darstellen: \begin{eqnarray}r=\frac{p}{1+\cos \varphi }.\end{eqnarray}

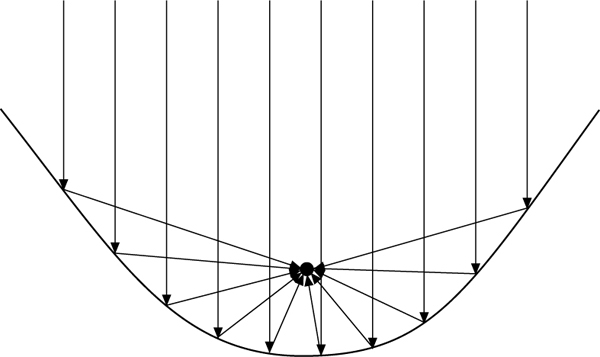
V. Brennpunkteigenschaft der Parabel. Strahlen, die parallel zur Achse einer Parabel einfallen, werden an der Parabel so reflektiert, daß sie durch den Brennpunkt F gehen, d. h., in jedem Punkt P einer Parabel halbiert die Tangente an die Parabel den Winkel zwischen der Geraden FP und der durch P verlaufenden Parallelen zur Parabelachse.

Umgekehrt werden Brennpunktstrahlen bei der Reflexion an einer Parabel zu Parallelstrahlen – eine Tatsache, die etwa bei Scheinwerfern Anwendung findet.