eine spezielle Lernregel für Neuronale Netze, die bereits gegen Ende der fünfziger Jahre von Frank Rosenblatt vorgeschlagen wurde und gewisse Defizite der Hebb-Lernregel kompensieren sollte; die Perceptron-Lernregel kann, etwas vereinfacht gesagt, als Delta-Lernregel für nicht differenzierbare Transferfunktionen angesehen werden.

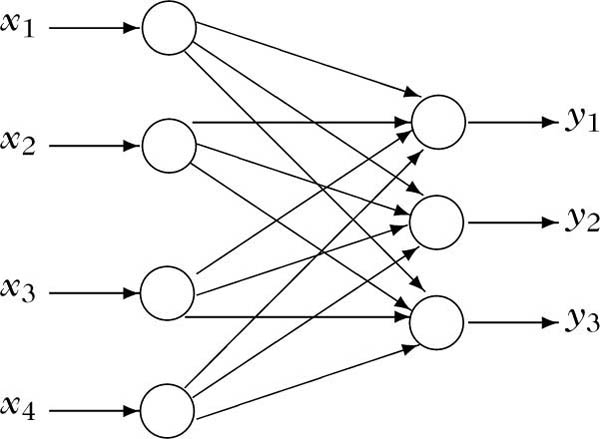
Im folgenden wird die prinzipielle Idee der Perceptron-Lernregel kurz im Kontext diskreter zweischichtiger neuronaler Feed-Forward-Netze mit Ridge-Typ-Aktivierung und nicht differenzierbarer sigmoidaler Transferfunktion in den Ausgabe-Neuronen erläutert (vgl. Abbildung):

Es sei T : ℝ → {0, 1} mit T(ξ) ≔ 0 für ξ< 0 und T(ξ) ≔ 1 für ξ ≥ 0 die für die Ausgabe-Neuronen des Netzes gegebene sigmoidale Transferfunktion. Wenn man diesem zweischichtigen Feed-Forward-Netz eine Menge von t Trainingswerten \begin{eqnarray}({x}^{(s)},{y}^{(s)})\in {{\mathbb{R}}}^{n}\times {\{0,1\}}^{m},\,\,\,\,1\le s\le t,\end{eqnarray} präsentiert, dann sollten die Gewichte w_ij ∈ ℝ, 1 ≤ i ≤ n, 1 ≤ j ≤ m, sowie die Schwellwerte Θ_j ∈ ℝ, 1 ≤ j ≤ m, so gewählt werden, daß für alle j ∈ {1,…,m} und für alle s ∈ {1,…,t} die quadrierten Fehler \begin{eqnarray}{\left({y}_{j}^{(s)}-T\left(\displaystyle \sum _{i=1}^{n}{w}_{ij}{x}_{i}^{(s)}-{{\rm{\Theta }}}_{j}\right)\right)}^{2}\end{eqnarray} möglichst klein werden.

Um dies zu erreichen, geht man bei der Perceptron-Lernregel wie folgt vor, wobei λ > 0 ein noch frei zu wählender sogenannter Lernparameter ist, der zum Teil in der Literatur fest auf λ = 1 gesetzt ist:

1. Gewichte w_ij, 1 ≤ i ≤ n, 1 ≤ j ≤ m: \begin{eqnarray}{w}_{ij}^{(neu)}:={w}_{ij}+\lambda ({y}_{j}^{(s)}-T(\displaystyle \sum _{k=1}^{n}{w}_{kj}{x}_{k}^{(s)}-{{\rm{\Theta }}}_{j})){x}_{i}^{(s)}.\end{eqnarray}

2. Schwellwerte Θ_j, 1 ≤ j ≤ m: \begin{eqnarray}{{\rm{\Theta }}}_{j}^{(neu)}:={{\rm{\Theta }}}_{j}-\lambda ({y}_{j}^{(s)}-T(\displaystyle \sum _{k=1}^{n}{w}_{kj}{x}_{k}^{(s)}-{{\rm{\Theta }}}_{j})).\end{eqnarray}

Die sukzessive Anwendung des obigen Verfahrens für alle s ∈ {1,…,t} und anschließende Iteration bezeichnet man nun als Perceptron-Lernregel. Es läßt sich zeigen, daß man nach endlich vielen Schritten des obigen Vorgehens ein perfekt auf den Trainingswerten arbeitendes Netz erhält (d.h. alle quadrierten Fehler sind Null), falls für alle j ∈ {1,…,m} die beiden Teilmengen \begin{eqnarray}{A}_{j}:=\{{x}^{(s)}|1\le s\le t\,\,\wedge \,\,{y}_{j}^{(s)}=0\}\end{eqnarray} und \begin{eqnarray}{B}_{j}:=\{{x}^{(s)}|1\le s\le t\,\,\wedge \,\,{y}_{j}^{(s)}=1\}\end{eqnarray} des ℝⁿ jeweils streng linear separierbar sind (Konvergenzsatz für die Perceptron-Lernregel).

Aufgrund dieses Resultats muß man also für eine gegebene Menge von Trainingswerten lediglich a priori sicherstellen, daß sie streng linear separierbar ist, um gewährleisten zu können, daß das Netz nach endlich vielen Lernschritten im Ausführ- Modus perfekt auf den Trainingswerten arbeitet. Eines der Probleme des Perceptron-Lernens besteht jedoch genau darin, daß es im allgemeinen ausgesprochen schwierig ist, einer gegebenen Menge von Trainingswerten anzusehen, ob sie streng linear separierbar ist oder nicht. Man müßte zum Beispiel Trennungsalgorithmen für konvexe Mengen einsetzen, wie sie in der Optimierung gebräuchlich sind, allerdings für den Preis eines erheblichen zusätzlichen Rechenaufwands.

Es drängt sich natürlich die Frage auf, was geschieht, wenn man ganz naiv die Perceptron-Lernregel ohne vorherigen Test auf strenge lineare Separierbarkeit anwendet. Im günstigsten Fall bricht das Perceptron-Lernen irgendwann ab, da das Netz perfekt auf den Trainingswerten arbeitet; die gegebene Menge von Trainingswerten ist streng linear separierbar. Im ungünstigsten Fall bricht das Perceptron-Lernen auch nach einer sehr großen Zahl von Iterationsschritten nicht ab, da immer noch einige Trainingswerte nicht beherrscht werden; die Menge der Trainingswerte ist vielleicht nicht streng linear separierbar, oder man hat nur zu früh mit dem Lernen aufgehört. Letztere Situation ist natürlich für die praktische Anwendung des Perceptron-Lernens ein ausgesprochenes Dilemma und Gegenstand verschiedenster Modifikationen und Verbesserungen.