Lexikon der Mathematik: Polyeder
auch Vielflächner genannt, ebenflächig begrenzter Körper.
Ein Polyeder ist eine beschränkte dreidimensionale Punktmenge des Raumes, die von endlich vielen ebenen Flächenstücken (n-Ecken) begrenzt wird. Gemeinsame Strecken verschiedener Begrenzungsflächen (Facetten) eines Polyeders werden Kanten, gemeinsame Eckpunkte von Begrenzungsflächen Ecken des Polyeders genannt. Zwischen der Anzahl der Ecken, Kanten und Begrenzungsflächen besteht ein Zusammenhang, der durch die Eulersche Polyederformel gegeben ist. Die Vereinigung aller Punkte der begrenzenden n-Ecke ist die Oberfläche des Polyeders, die gewöhnlich als Teilmenge des Polyeders aufgefaßt wird. Ein Polyeder heißt konvex, falls es zu jeweils zwei beliebigen seiner Punkte auch alle Punkte ihrer Verbindungsstrecke enthält. Sind alle Kanten eines konvexen Polyeders gleich lang, und treffen sich an jeder Polyederecke gleich viele Seitenflächen, so handelt es sich um ein reguläres Polyeder.
In algebraischer Formulierung ist ein Polyeder eine Teilmenge des ℝn, die sich in der Form
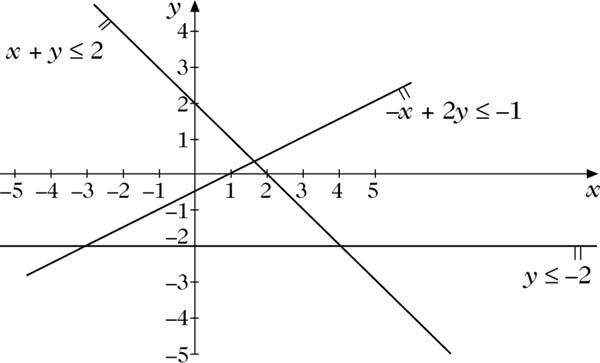
Polyeder
Die Abbildung zeigt das Polyeder
Ein konvexes Polyeder kann auch als beschränkte Durchschnittsmenge endlich vieler abgeschlossener Halbräume definiert werden.
Eine Verallgemeinerung des Polyeders ist das n-dimensionale Polytop.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.