die zu einer Zahl p ∈ ℝ, dem Exponenten, durch \begin{eqnarray}{x}^{p}={\text{pot}}_{p}(x)=\exp (p\,\mathrm{ln}\,x) & (x\in (0,\infty ))\end{eqnarray} definierte Funktion pot_p : (0, ∞) → (0, ∞).

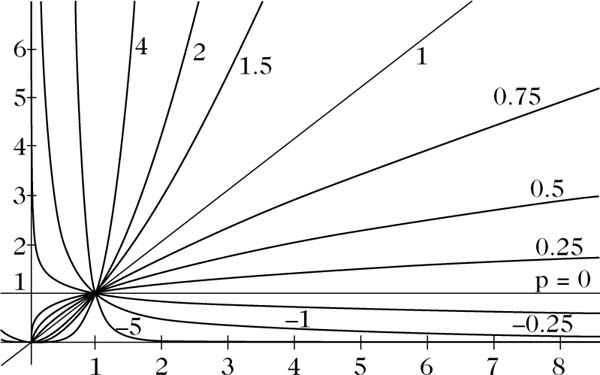
Diese Definition ist konsistent mit der Definition der Potenzenx^k für k ∈ ℤ durch iterierte Multiplikation. Aus der Differenzierbarkeit von exp und ln und der Kettenregel folgt die Differenzierbarkeit von pot_p, und mit exp′ = exp und ln′ \(x=\frac{1}{x}\) erhält man (x^p)′ = px^p−1, d. h. pot′_p = p pot_p−1. Daher ist die Potenzfunktion zum Exponenten p streng antiton für p< 0, konstant 1 für p = 0 und streng isoton für p< 0. Für p< 0 gilt x^p → ∞ für x ↓ 0 und x^p → 0 für x → ∞, für p > 0 hat man x^p → 0 für x ↓ 0 und x^p → ∞ für x → ∞. Insbesondere ist pot_p für p ≠ 0 bijektiv.

Aus den Eigenschaften der Exponentialfunktion und der Logarithmusfunktion erhält man für p, q ∈ ℝ und x, y ∈ (0, ∞) u. a. die Identitäten (xy)^p = x^p y^p, (1/x)^p = 1/x^p = x^−p, x^px^q = x^p+q und (x^p)^q = x^pq, also für a ∈ (0, ∞): \begin{eqnarray}{x}^{p}=a\iff {x}^{p}={a}^{\frac{1}{p}}\end{eqnarray} Insbesondere gilt \({x}^{\frac{1}{k}}=\sqrt[k]{x}\) für k ∈ ℕ, d. h. die Potenzfunktion zum Exponenten \(\frac{1}{k}\) ist gerade die k-te Wurzelfunktion.

Die Potenzfunktion läßt sich auch für komplexe Argumente definieren. Dies entweder als mengentheoretische Funktion oder, nach Wahl etwa des Hauptzweigs der Logarithmusfunktion, wie oben.