spielt eine wichtige Rolle bei der Untersuchung des Randverhaltens konformer Abbildungen.

Zur Definition sind einige Vorbereitungen nötig. Sei G ⊂ ℂ ein beschränktes, einfach zusammenhängendes Gebiet. Weiter sei \(\gamma \ :\ [0,1]\ \to \ \bar{G}\) ein Weg in \(\bar{G}\) derart, daß \begin{eqnarray}\gamma ({t}_{1})\ \ne \ \gamma ({t}_{2})\ \text{f}\mathrm{\ddot{u}}\text{r}\ \text{0}\ \lt \ {\text{t}}_{1}\ \lt \ {t}_{2}\ \lt \ 1\end{eqnarray} und \begin{eqnarray}\gamma \ ([0,1])\ \cap \ \partial G\ =\ \{\gamma \ (0),\ \gamma \ (1)\}.\end{eqnarray} Dabei ist γ (0) = γ (1) erlaubt.

Dann heißt C := γ ((0, 1)) ein Querschnitt in G. Die Menge G \ C besitzt genau zwei Zusammenhangskomponenten G₁, G₂, und es gilt \begin{eqnarray}G\ \cap \ \partial {G}_{1}\ =\ G\ \cap \ \partial {G}_{2}\ =\ C.\end{eqnarray} Eine Nullkette (C_n) von G ist eine Folge von Querschnitten C₀, C₁, C₂,… in G mit folgenden Eigenschaften:

• 1. Art, falls Π(p) einpunktig ist und Π(p) = I(p),
• 2. Art, falls Π(p) einpunktig ist und Π(p) ≠ I(p),
• 3. Art, falls Π(p) nicht einpunktig ist und Π(p) = I(p),
• 4. Art, falls Π(p) nicht einpunktig ist und Π(p) ≠ I(p).

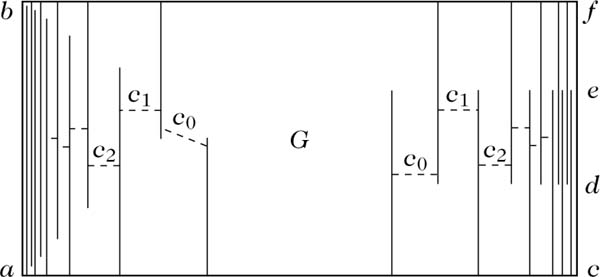
Die Abbildungen zeigen einige Beispiele für Primenden.

Zur Anwendung der Primendentheorie siehe Randverhalten konformer Abbildungen.