Quantile-Quantile-Plot, Methode der deskriptiven Statistik zur graphischen Überprü-fung einer Hypothese über die unbekannte Wahrscheinlichkeitsverteilung einer ein- oder mehrdimensionalen Zufallsgröße X.

Dabei werden die in einer Stichprobe beobachteten tatsächlichen Häufigkeiten (bzw. Quantile) den bei Vorliegen der Verteilung erwarteten Häufigkeiten (Quantilen) in Form eines Streudiagramms gegenübergestellt. Andere, ähnliche, graphische Methoden zur Überprüfung einer Hypothese über eine Verteilung sind z. B. die P-P-Plots oder das Wahrscheinlichkeitspapier.

Es soll beispielsweise die Hypothese überprüft werden, ob die Verteilung eines p-dimensionalen Merkmalsvektors \(\overrightarrow{X}=({X}_{1},\mathrm{...},{X}_{p})\), der an bestimmten Objekten einer Grundgesamtheit beobachtet wird, wesentlich von einer p-dimensionalen Normalverteilung abweicht oder nicht. Zur Überprüfung dieser Hypothese mittels Q-Q-Plots führt man zunächst eine Stichprobe \({\overrightarrow{X}}_{i}\) = 1, …, n, vom Umfang n durch, berechnet das Stichprobenmittel \(\overrightarrow{\overline{X}}\) und die Stichproben-Kovarianzmatrix \(\hat{S}\), und daraus die (quadratischen) Mahalanobis-Abständed_i der n Beobachtungsvektoren \({\overrightarrow{X}}_{i}\)i = 1, …, n, vom Sichprobenmittel \(\overrightarrow{\overline{X}}\):

\begin{eqnarray}{d}_{i}={({\overrightarrow{X}}_{i}-\overrightarrow{\overline{X}})}^{T}{S}^{-1}({\overrightarrow{X}}_{j}-\overrightarrow{\overline{X}})\,\text{f}{\rm\ddot{u}}\text{r}\,i=1,\mathrm{...},n.\end{eqnarray}

Sind die Daten multivariat normalverteilt, so genügen die Abstände d₁, …, d_n approximativ einer χ² -Verteilung mit p Freiheitsgraden.

Ordnet man nun die Abstände der Größe nach, \begin{eqnarray}{d}_{(1)}\le {d}_{(2)}\le \mathrm{...}\le {d}_{(n)},\end{eqnarray}

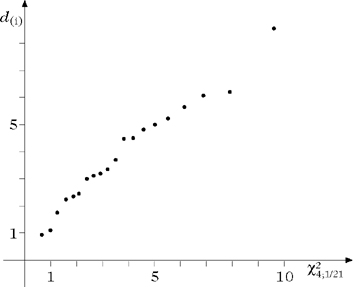
und bestimmt die (i/(n + 1))-Quantile \({\chi }_{p;i/(n+1)}^{2}\) für i = 1, …, n, so liegen die n Punkte \(({\chi }_{p;i/(n+1)}^{2},{d}_{(i)}),\), i = 1, …, n, die gerade den Q-Q-Plot bilden, in etwa auf einer Geraden mit der Steigung 1 durch den Ursprung. Die Abbildung zeigt ein Beispiel hierzu, nämlich die Q-Q-Plots für n = 20 Beobachtungen, die zufällig aus einer 4-dimensionalen Normalverteilung (p = 4) durch Simulation erzeugt wurden. Man sieht deutlich, daß die beobachteten und erwarteten Quantile tatsächlich nahezu auf einer Geraden liegen.