Lexikon der Mathematik: QR-Zerlegung
Zerlegung einer Matrix A ∈ ℝm×n in ein Produkt A = QR, wobei Q ∈ ℝm×m orthogonal und R ∈ ℝm×n eine obere Dreiecksmatrix ist.
Hat A vollen Spaltenrang, also Rang(A) = n, so existiert eine QR-Zerlegung A = QR mit rii > 0. Diese Zerlegung ist eindeutig.
Das Ergebnis einer Orthonormalisierung von n gegebenen Vektoren xj ∈ ℝm kann als QR-Zerlegung der Matrix X = (x1, x2, …, xn) ∈ ℝm×n interpretiert werden.
Eine häufig verwendete Möglichkeit der Berechnung einer QR-Zerlegung besteht in der Verwendung von Householder-Matrizen
mit vT v = 1.
Mit Hilfe der Householder-Matrizen kann man eine Matrix A = (a1, …, an) ∈ ℝm×n in eine obere Dreiecksmatrix transformieren, indem sukzessive die Elemente unterhalb der Diagonalen eliminiert werden. Im ersten Schritt werden die Elemente der ersten Spalte von A unterhalb des Diagonalelementes a11 eliminiert gemäß
wobei \({Q}^{(1)}=I-2{v}_{1}{v}_{1}^{T}\) mit
und λ1 = −sgn(a11)∥a1∥2, falls a11 ≠ 0, sonst λ1 = −∥a1∥2. Im zweiten Schritt werden nun ganz analog die Elemente der zweiten Spalte von A(1) unterhalb des Diagonalelementes a22 eliminiert:
Nach dem k-ten Schritt hat man somit die Ausgangsmatrix A bis auf eine Restmatrix T(k+1) ∈ ℝ(m−k)×(n−k) auf obere Dreiecksgestalt gebracht,
Bildet man nun die orthogonale Matrix
wobei \({\overline{Q}}^{(k+1)}\in {{\mathbb{R}}}^{(m-k)\times (m-k)}\) wie im ersten Schritt mit T(k+1) anstelle von A konstruiert wird, so kann man die nächste Subspalte unterhalb der Diagonalen eliminieren. Insgesamt erhält man so nach p = min(m − 1, n) Schritten die obere Dreiecksmatrix
und daher wegen (Q(j))2 = I die Zerlegung
Für den Aufwand gilt bei dieser Methode
a) ∼ 2n2m Multiplikationen, falls m ≫ n,
b) \(\sim\frac{2}{3}{n}^{3}\) Multiplikationen, falls m ≈ n.
Eine andere Möglichkeit zur Berechnung einer QR-Zerlegung von A besteht in der Anwendung von Givens-Matrizen (Jacobi-Rotationsmatrix) Gkℓ zur sukzessiven spaltenweisen Elimination der Einträge unterhalb der Diagonalen von A. Dabei wird Gkℓ so gewählt, daß in GkℓA ein gewisses Element in der k-ten Zeile zu Null wird. Am Beispiel einer vollbesetzten (5 × 4)-Matrix läßt sich der Algorithmus wie folgt veranschaulichen (die Indexpaare (k,ℓ) über den Pfeilen geben die Indizes der ausgeführten Givens-Rotation Gkℓ an):
Allgemein erhält man
Für k = 1, …, n
Für ℓ = m, m − 1, …, k + 1
Berechne Gℓ,ℓ−1 so daß (Gℓ,ℓ−1A)ℓ, k = 0.
Berechne A := Gℓ,ℓ−1A.
Ende Für
Ende Für
Setze QT = Gm, m−1 …Gm−1, m−2Gm, m−1.
Dies berechnet
In der Praxis werden nicht die (m × m)-Matrizen Gℓ,ℓ−1 aufgestellt, sondern nur die entsprechenden Umformungen der Elemente von A in der ℓ-ten und (ℓ − 1)-ten Zeile vorgenommen.
Als Aufwand für die QR-Zerlegung einer vollbesetzten Ausgangsmatrix A ∈ ℝm×n erhält man hier
a) ∼ mn Quadratwurzeln und ∼ 2mn2 Multiplikationen, falls m ≫ n,
b) ∼ n2 /2 Quadratwurzeln und ∼ 4n3 /3 Multiplikationen, falls m ≈ n.
Für Matrizen A ∈ ℂ m×n existiert ebenfalls eine QR-Zerlegung A = QR, wobei Q ∈ ℂm×m unitär und R ∈ ℂm×n eine obere Dreiecksmatrix ist. Sie wird analog zum obigen Vorgehen berechnet. Man verwendet die komplexen Varianten der Householderoder Givens-Matrizen.
Die QR-Zerlegung kann zur direkten Lösung linearer GleichungssystemeAx = b verwendet werden. Sie hat große Bedeutung bei der Lösung des linearen Ausgleichsproblems ||Ax − b||2 mittels der Methode der kleinsten Quadrate und des Eigenwertproblems Ax = λx mittels des QR-Algorithmus’.
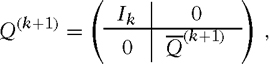
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.