Lexikon der Mathematik: Rademacher-Funktionen
das System (Rn)n∈ℕ der Funktionen Rn : [0, 1) →{− 1, 1} mit
\begin{eqnarray}{R}_{n}(x)=2\cdot {\bf{1}}_{{A}_{n}}(x)-1,\end{eqnarray}
wobei 1An für jedes n ∈ ℕ die Indikatorfunktion der Menge
\begin{eqnarray}{A}_{n}=\displaystyle \underset{k=1}{\overset{{2}^{n-1}}{\cup }}\left[\displaystyle \frac{2k-1}{{2}^{n}},\displaystyle \frac{2k}{{2}^{n}}\right)\end{eqnarray}
bezeichnet.
Eine andere Definition ist durch
\begin{eqnarray}{R}_{n}(t)=\text{sign}(\sin {2}^{n}\pi t)\end{eqnarray}
gegeben.
Rademacher-Funktionen haben Anwendungen in der Theorie orthogonaler Reihen sowie der Wahrscheinlichkeitstheorie.
Zerlegt man die Zahl x ∈ [0, 1) in einen Dualbruch
\begin{eqnarray}\begin{array}{cc}x=\displaystyle \sum _{k=1}^{\infty }\displaystyle \frac{{x}_{k}}{{2}^{k}}, & {x}_{k}\in \{0,1\},\end{array}\end{eqnarray}
wobei aus Gründen der Eindeutigkeit nur Zerlegungen mit xk = 0 für unendlich viele k ∈ ℕ betrachtet werden, so gilt Rn (x) = 1 genau dann, wenn xn = 1 ist.
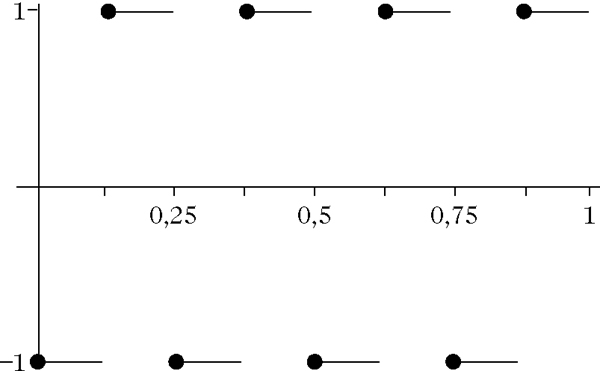
Graph der Rademacher-Funktion R3
Das System (Rn)n∈ℕ der Rademacher-Funktionen ist orthonormiert, d. h., für alle m, n ∈ ℕ gilt
\begin{eqnarray}\displaystyle \underset{0}{\overset{1}{\int }}{R}_{m}(x){R}_{n}(x)dx={\delta }_{mn}.\end{eqnarray}
Man bezeichnet es auch als Rademacher-System.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.