Lexikon der Mathematik: Rayleigh-Verteilung
bei gegebenem Parameter σ > 0 das durch die Wahrscheinlichkeitsdichte
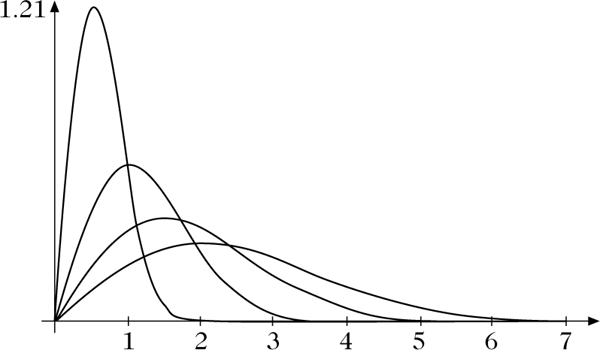
Dichten der Rayleigh-Verteilungen mit Parametern σ = 0.5(0.5)2.0
Besitzt die Zufallsvariable X eine Rayleigh-Verteilung mit dem Parameter σ > 0, so gilt für den Erwartungswert \(E(X)=\sigma \sqrt{\pi /2}\) und für die Varianz \(Var(X)=\frac{1}{2}{\sigma }^{2}(4-\pi )\). Der Modalwert liegt an der Stelle x = σ, und der Median ist \(m=\sigma \sqrt{\mathrm{ln}\,4}\). Die Rayleigh-Verteilung ist eine spezielle Weibull-Verteilung.
Anwendungen der Rayleigh-Verteilung finden sich z. B. in den Ingenieurwissenschaften, wo sie etwa zur Modellierung der Lebensdauer von schnell alternden Bauteilen verwendet wird.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.