Menge der Primideale im (kommutativen) Ring R so, daß die Lokalisierung nach diesen Primidealen ein regulärer Ring ist.

Geometrisch ist der reguläre Ort die Menge der regulären Punkte, d. h. die Menge der Punkte, in denen die Dimension des Tangentialraums gleich der Dimension der Varietät ist.

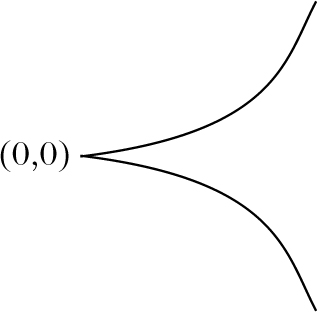
Ist beispielsweise \(R={\mathbb{C}}[x,y]/({x}^{2}-{y}^{3})\), dann ist R regulär für alle Primideale von R, die verschieden vom Ideal (x, y) sind. R_{(x, y)} ist nicht regulär. Geometrisch bedeutet das, daß \begin{eqnarray}V=\{(x,y)\in {{\mathbb{C}}}^{2}:{x}^{2}={y}^{3}\}\end{eqnarray} in allen Punkten bis auf den Nullpunkt regulär ist (vgl. Abbildung).