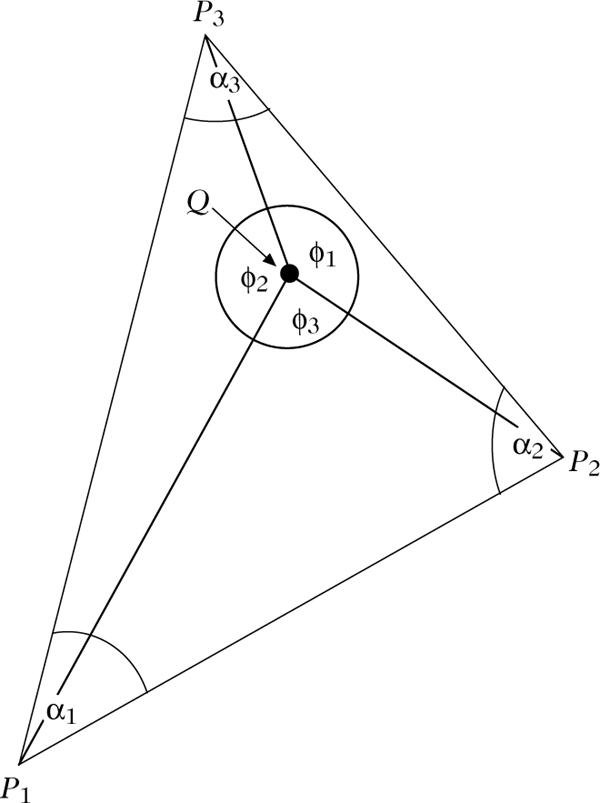
geodäsisches Verfahren zur Bestimmung der Koordinaten eines Punktes Q(x, y) aus denen dreier bekannter Punkte P₁(x₁, y₁), P₂(x₂, y₂) und P₃(x₃, y₃) durch Messung der Winkel \({\phi }_{1}=\angle ({P}_{2}Q{P}_{3}),{\phi }_{2}=\angle ({P}_{1}Q{P}_{3})\) und \({\phi }_{3}=\angle ({P}_{1}Q{P}_{2})\) zwischen den von Q ausgehenden Strahlen in Richtung der bekannten Punkte.

Dazu darf allerdings Q nicht auf dem Umkreis des Dreiecks ΔP₁P₂P₃ liegen. Der Punkt Q kann dann als Schnittpunkt dreier Ecktransversa-len P₁Q, P₂Q und P₃Q des Dreiecks ΔP₁P₂P₃ (mitden Innenwinkeln α₁, α₂ und α₃) aufgefaßt werden, und es gilt: \begin{eqnarray}\begin{array}{rcl}x & = &\displaystyle\frac{{g}_{1}{x}_{1}+{g}_{2}{x}_{2}+{g}_{3}{x}_{3}}{{g}_{1}+{g}_{2}+{g}_{3}}\quad \text{und}\\ y & = &\displaystyle\frac{{g}_{1}{y}_{1}+{g}_{2}{y}_{2}+{g}_{3}{y}_{3}}{{g}_{1}+{g}_{2}+{g}_{3}}\quad \text{mit}\\ {g}_{1} & = &\displaystyle\frac{1}{\cot {\alpha }_{1}-\cot {\phi }_{1}}, & \\ {g}_{2} & = &\displaystyle\frac{1}{\cot {\alpha }_{2}-\cot {\phi }_{2}} \quad\text{und}\\ {g}_{3} & = &\displaystyle\frac{1}{\cot {\alpha }_{3}-\cot {\phi }_{3}}. & \end{array}\end{eqnarray}