Lexikon der Mathematik: Runge-Funktion
Funktion, die die Inflexibilität der Lagrange-Interpolation mit Polynomen hohen Grades zeigt.
Die Funktion f : [−5, 5] ↦ ℝ, definiert durch
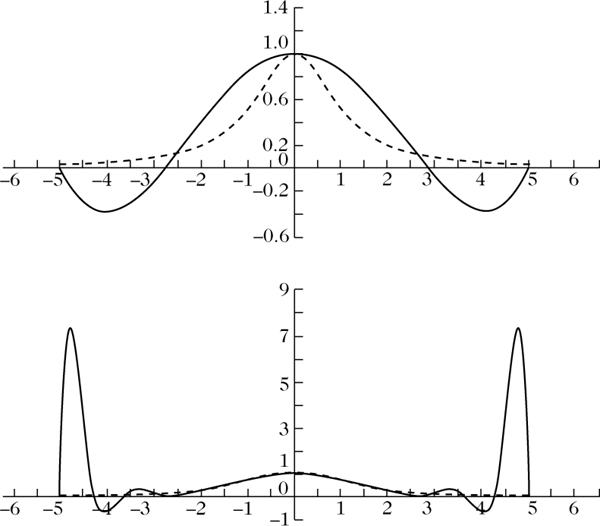
Interpolation der Runge-Funktion (gestrichelt) an 5 (oben) und 15 (unten) Interpolationsstellen.
Es sei \(a\le {t}_{0}^{(m)}\lt \ldots \lt {t}_{m}^{(m)}\le b, m\in {\mathbb{N}}\), eine Folge von Interpolationspunkten. Dann existiert eine Funktion f ∈ C[a, b] so, daß
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.