wichtiger Satz in der Funktionentheorie, der wie folgt lautet:

Es sei \(K\subset {\mathbb{C}}\)eine kompakte Menge derart, daß ℂ\K zusammenhängend ist. Weiter sei D ⊂ ℂ eine offene Menge mit D ⊃ K.

Dann existiert zu jeder in D holomorphen Funktion f eine Folge (p_n) von Polynomen, die gleichmäßig auf K gegen f konvergiert.

Falls ℂ\K nicht zusammenhängend ist, so gilt die Aussage im allgemeinen nicht mehr. Dies sieht man leicht an dem Beispiel \(K=\{z\in {\mathbb{C}}:|z|=1\}\) und \(f(z)=\frac{1}{z}\). Siehe hierzu Runge, Approximationssatz von.

Im folgenden wird noch eine Anwendung des kleinen Satzes von Runge gegeben. Es ist leicht, eine Folge (f_n) von in ℂ stetigen Funktionen anzugeben, die in ℂ punktweise konvergiert, aber deren Grenzfunktion an 0 unstetig ist, z. B. \begin{eqnarray}{f}_{n}(z)=\frac{1}{1+n|z|}.\end{eqnarray} Verlangt man aber, daß jedes f_n in ℂ holomorph sein soll, so scheint folgende Konstruktion mit Hilfe des Satzes von Runge die einfachste zu sein.

Für a ∈ ℂ, r > 0 und E ⊂ ℂ sei \begin{eqnarray}{B}_{r}(a):=\{z\in {\mathbb{C}}:|z-a|\lt r\}\end{eqnarray} und \begin{eqnarray}\text{dist}(a, E):=\mathop{\inf }\limits_{z\in E}|a-z|.\end{eqnarray} Für \(n\in {\mathbb{N}}\) sei \begin{eqnarray}{I}_{n}:=\left\{z\in {B}_{n}(0):\text {dist}(z,[0,\infty ))\gt \frac{1}{n}\right\}\end{eqnarray} und \({K}_{n}:=\{0\}\mathop{\cup }\limits^{}\left[\frac{1}{n}, n\right]\mathop{\cup }\limits^{}{\overline{I}}_{n}\). Dann ist K_n kompakt und ℂ\K_n zusammenhängend. Weiter sei ε_n > 0 so klein gewählt, daß die offenen Mengen \begin{eqnarray}{B}_{n}:={B}_{\varepsilon }{}_{{}_{n}}(0),\quad A_n:=\mathop{\bigcup }\limits_{x\in \left[\frac{1}{n}, n\right]}{B}_{\varepsilon }{}_{{}_{n}}(x),\quad{I}_{n+1}\end{eqnarray} paarweise disjunkt sind. Dann ist \({D}_{n}:={B}_{n}\mathop{\cup }\limits^{}{A}_{n}\mathop{\cup }\limits^{}{I}_{n+1}\) eine offene Menge mit \({D}_{n}\supset {K}_{n}\). Zur Verdeutlichung der Konstruktion vergleiche man die Abbildung.

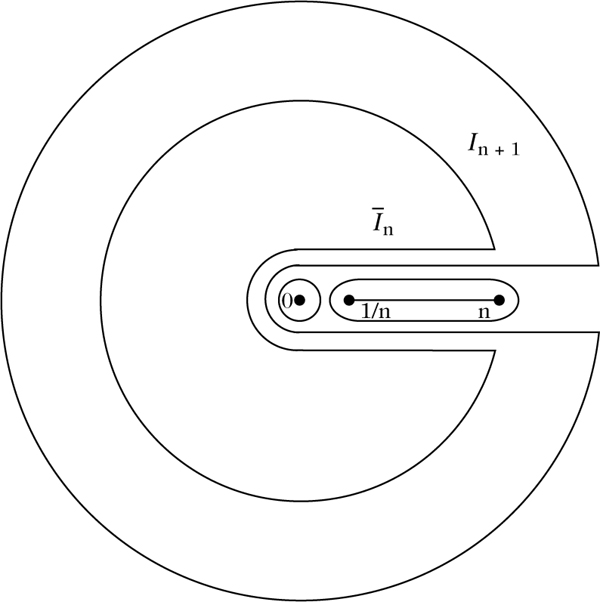
Durch g_n(z) := 1 für z ∈ B_n und g_n(z) := 0 für \(z\in {A}_{n}\mathop{\cup }\limits^{}{I}_{n+1}\) wird eine in D_n holomorphe Funktion definiert. Nach dem kleinen Satz von Runge gibt es nun ein Polynom p_n mit \begin{eqnarray}|{p}_{n}(z)-{g}_{n}(z)|\lt \frac{1}{n}\end{eqnarray} für alle z ∈ K_n. Die Folge (p_n) hat folgende Eigenschaften:

1. \(\mathop{\mathrm{lim}}\limits_{n\to \infty }{p}_{n}(0)=1\).
2. \(\mathop{\mathrm{lim}}\limits_{n\to \infty }{p}_{n}(z)=0\) für alle \(z\in {\mathbb{C}}\backslash \{0\}\).
3. Die Folge (p_n) ist in \({\mathbb{C}}\backslash [0,\infty )\) kompakt konvergent (kompakt konvergente Folge).
4. Die Folge (p_n) ist in keiner Kreisscheibe B_δ(x) mit x ≥ 0 und Δ > 0 kompakt konvergent.