Lexikon der Mathematik: Runge-Kutta-Methode
Klasse von Einschritt-verfahren zur näherungsweisen Lösung von Anfangswertaufgaben gewöhnlicher Differentialgleichungen der Form \({y}{^{\prime} }=f(x, y), y({x}_{0})={y}_{0}\).
Explizite Runge-Kutta-Methoden leiten sich mit einer äquidistanten Unterteilung \({x}_{k}={x}_{0}+kh\) mit Schrittweite h aus der zugehörigen Integralgleichung
Die Koeffizienten von Runge-Kutta-Methoden werden üblicherweise in der Form
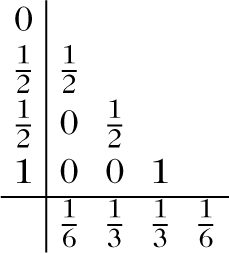
notiert. Für die klassische Runge-Kutta-Methode ergeben sich bei s = 4 z. B. die Werte
Bei impliziten Runge-Kutta-Methoden werden die Stützstellen allgemeiner durch
Unter den s-stufigen impliziten Runge-Kutta-Methoden befinden sich solche mit bestimmten Stabilitätseigenschaften, die sie für steife Differentialgleichungssysteme geeignet machen.
[1] Lambert, J.D.: Numerical methods for ordinary differential systems. John Wiley and Sons Chichester, 1991.
[2] Schwetlick, H.; Kretzschmar, H.: Numerische Verfahren für Naturwissenschaftler und Ingenieure. Fachbuchverlag Leipzig, 1991.
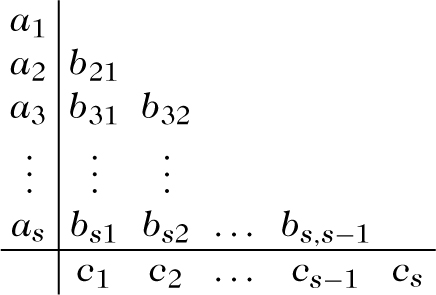
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.