Lexikon der Mathematik: Schauder-Basis
eine Folge b1, b2,… eines separablen Banachraums X so, daß jedes Element x ∈ X auf eindeutige Weise als konvergente Reihe
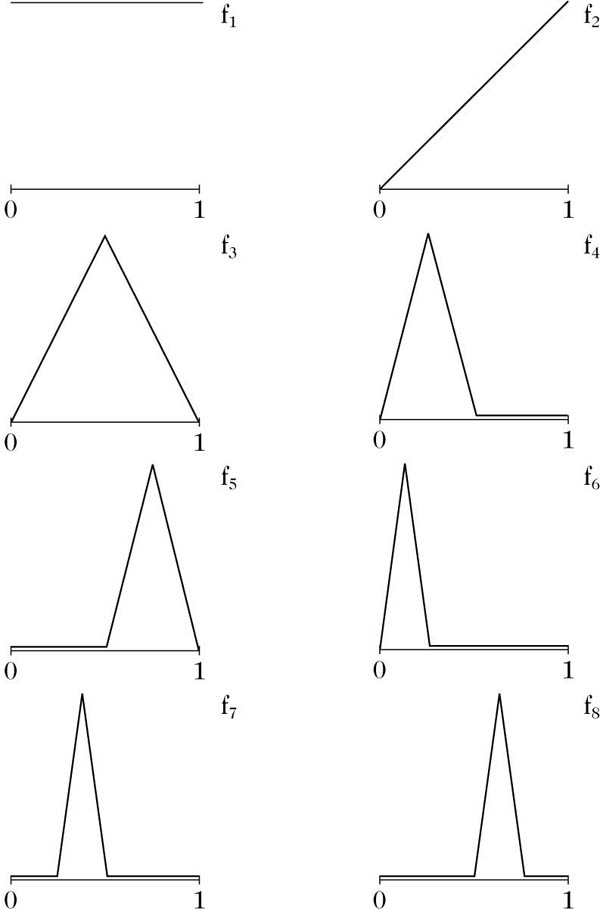
Das Schaudersche Funktionensystem in C[0, 1]
Schauder konstruierte 1927 folgende Schauder-Basis des Banachraums C[0, 1] (Schaudersches Funktionensystem): Es ist f1(t) = 1, f2(t) = t, und die weiteren Basisfunktionen sind „Dreiecksfunktionen“; ihr Bildungsgesetz ist den Graphen von f3, …,f8 zu entnehmen.
Nicht jeder separable Banachraum hat eine Schauder-Basis, jedoch gibt es stets einen unendlichdimensionalen Unterraum mit einer Schauder-Basis. Ein Beispiel von Gowers und Maurey (1993) zeigt hingegen, daß es nicht notwendig einen unendlichdimensionalen Unterraum mit einer unbedingten Basis gibt.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.