ein Punkt einer regulären ebenen Kurve α(s), in dem die Ableitung dκ(s)/ds der Krümmungsfunktion κ(s) nach dem Kurvenparameter 0 ist.

Eine Kurve heißt geschlossen, wenn die Komponenten von κ(s) periodische Funktionen sind. Eines der ersten Resultate der Differentialgeometrie im Großen ist der Vierscheitelsatz:

Eine geschlossene Kurve mit positiver Krümmung hat mindestens vier Scheitelpunkte.

Die Ellipse mit den Halbachsen a und b hat die parametrische Gleichung β(t) = (a sin(t), b sin(t)). Ihre Krümmung κ(t) und deren Ableitung κ′(t) sind die Funktionen \begin{eqnarray}\begin{array}{lll}\kappa (t) & = & \frac{ab}{\sqrt{{({b}^{2}\cos t+{a}^{2}\sin t)}^{3}}},\\ {\kappa }^{\prime}(t) & = & \frac{3\,a\,b\,({b}^{2}-{a}^{2})\,\sin (2\,t)}{2\sqrt{{({b}^{2}\cos t+{a}^{2}\sin t)}^{5}}}.\end{array}\end{eqnarray}

Somit verschwindet κ′(t) im Fall a ≠ b für die vier Werte t = k π/2 (k = 0, l, 2, 3), die den Kurvenpunkten (±a, 0) und (0, ±b) entsprechen. Für a = b ergibt sich eine Kreislinie, die nur aus Scheitelpunkten besteht.

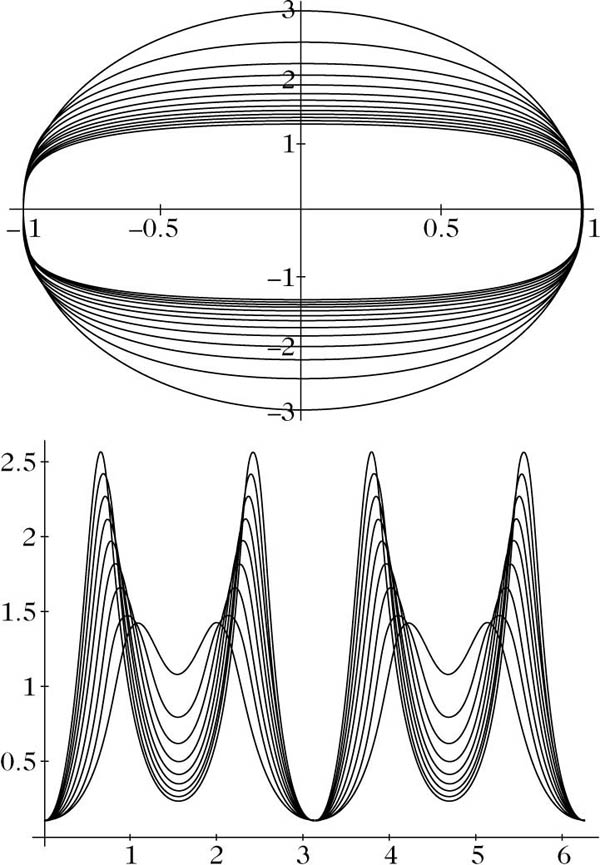
Ein anderes Beispiel liefern die Sinusovale \begin{eqnarray}{\sigma }_{n}(t)=(a\,\cos t,\,\,b\,{\sin }^{\{n\}}(t)),\end{eqnarray} worin die Funktion sin^{n}(t) die n-te Iteration \begin{eqnarray}{\sin }^{\{n\}}(t)=\mathop{\underbrace{\sin (\sin (\ldots \sin (\sin }}\limits_{n}(t\mathop{\underbrace{))\ldots ))}}\limits_{n}\end{eqnarray} bezeichnet. Die Abbildung zeigt die Sinusovale σ_n(t) zusammen mit ihren Krümmungsfunktionen für n = 3, …, 11. Man erkennt, daß sie für n ≥ 3 acht Scheitelpunkte haben.

Der Scheitelpunkt S = (0, 0) der Parabel γ(t) = (t, p t²) wird meist im Zusammenhang mit einer elementargeometrischen Konstruktion definiert, S ist aber auch im Sinne der hier gegebenen allgemeinen Definition ein Scheitelpunkt der Parabel.